Закон Ампера. Взаимодействие параллельных токов

Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, ис­пытываемый рамкой, есть результат дейст­вия сил на ее отдельные элементы. Обоб­щая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила (dF, с которой магнитное поле действует на элемент проводника dl с током, находяще­гося в магнитном поле, прямо пропорцио­нальна силе тока I в проводнике и век­торному произведению элемента длиной dl проводника на магнитную индук­цию В:

dF = I[dl,В]. (1)

Направление вектора dF может быть найдено, согласно (1), по общим пра­вилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера вычисляется по формуле

(2)

где a - угол между векторами dl и В.

Закон Ампера применяется для опре­деления силы взаимодействия двух токов. Рассмотрим два бесконечных прямолиней­ных параллельных тока I₁ и I₂ (направле­ния токов указаны на рис. 1), расстоя­ние между которыми равно R. Каждый из проводников создает магнитное поле, ко­торое действует по закону Ампера на дру­гой проводник с током. Рассмотрим, с ка­кой силой действует магнитное поле тока I₁ на элемент dl второго проводника с то­ком I₂. Ток I₁ создает вокруг себя магнит­ное поле, линии магнитной индукции кото­рого представляют собой концентрические окружности. Направление вектора В | за­дается правилом правого винта, его мо­дуль равен

рис. 1

Направление силы dF₁, с которой поле В ₁ действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, со­гласно (2), с учетом того, что угол ее между элементами тока I₂ и вектором B₁ прямой, равен

или, подставляя значение для B₁, получим

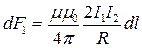(3)

Рассуждая аналогично, можно пока­зать, что сила d F ₂, с которой магнитное поле тока I₂ действует на элемент dl пер­вого проводника с током I₁, направлена в противоположную сторону и по модулю равна

(4)

Сравнение выражений (3) и (4) показывает, что

т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой

. (5)

Если токи имеют противоположные на­правления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяе­мая формулой (5).

Если два параллельных проводника с то­ком находятся в вакууме (m=l), то сила взаимодействия на единицу длины про­водника, согласно (5), равна

(6)

Для нахождения числового значения m₀ воспользуемся определением ампера, согласно которому при I₁=I₂=1A и R=1 м . Подставив это значение в формулу (6), получим

m₀ = 4p×10^-7 Н/А² = 4p×10^-7 Гн/м,

где генри (Гн) - единица индуктивности

Магнитное поле

Движущегося заряда

Каждый проводник с током создает в ок­ружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что лю­бой движущийся в вакууме или среде за­ряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий по­ле В точечного заряда Q, свободно движу­щегося е нерелятивистской скоростью v. Под свободным движением заряда по­нимается его движение с постоянной ско­ростью. Этот закон выражается формулой

(1)

где r – радиус-вектор, проведенный от за­ряда Q к точке наблюдения. Согласно выражению (1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и r, а именно: его направление совпадает с на­правлением поступательного движения правого винта при его вращении от v к r. Модуль магнитной индукции (1) вычисляется по формуле

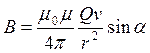(2)

где a – угол между векторами v и r.

Сравнивая 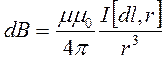и (1), видим, что движущийся заряд по своим магнитным свойствам эквива­лентен элементу тока:

Idl = Qv.

Закономерности (1) и (2) справедливы лишь при малых скоростях (v<<с) движущихся зарядов, когда электрическое поле свободно движу­щегося заряда можно считать электроста­тическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени находится дви­жущийся заряд.

Не нашли, что искали? Воспользуйтесь поиском: