Действие магнитного поля на движущийся заряд

Опыт показывает, что магнитное поле дей­ствует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, дей­ствующая на электрический заряд Q, дви­жущийся в магнитном поле со скоростью v, называется силой Лоренца и выражает­ся формулой

F =Q[ vB ], (1)

где В – индукция магнитного поля, в котором движется заряд.

Направление силы Лоренца определя­ется с помощью правила левой руки: если ладонь левой руки расположить так, что­бы в нее входил вектор В, а четыре вы­тянутых пальца направить вдоль вектора v, то отогнутый большой палец покажет на­правление силы, действующей на положи­тельный заряд. На отрицательный заряд сила действует в противоположном направлении.

Модуль силы Лоренца равен

,

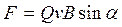где a – угол между v и В.

Маг­нитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрическо­го. Магнитное поле действует только на движущиеся в нем заряды.

Сила Лоренца всегда перпендикуляр­на скорости движения заряженной части­цы, поэтому она изменяет только направ­ление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Значит, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изме­няется.

Если на движущийся электрический заряд помимо магнитного поля с индук­цией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил – силы, действующей со стороны электрического поля, и силы Ло­ренца:

.

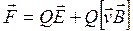Это выражение называется формулой Ло­ренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.

Движение заряженных частиц в магнитном поле

Выражение для силы Лоренца по­зволяет найти ряд закономерностей дви­жения заряженных частиц в магнитном поле. Направление силы Лоренца и на­правление вызываемого ею отклонения за­ряженной частицы в магнитном поле за­висят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Будем считать, что магнитное поле одно­родно, и на частицы электрические поля не действуют. Если заряженная частица дви­жется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В ра­вен 0 или p. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она дви­жется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца F =Q[ vB ] постоянна по модулю и нор­мальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяет­ся из условия

,

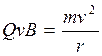откуда

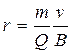(1)

Период вращения частицы T,

.

Подставив сюда выражение (1), по­лучим

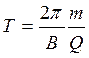, (2)

т. е. период вращения частицы в однород­ном магнитном поле определяется только величиной, обратной удельному заряду (Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v <<С).

Рис. 1

Если скорость v заряженной частицы направлена под углом a к вектору В (рис.1), то ее движение можно пред­ставить в виде двух движений: 1) равно­мерного прямолинейного движения вдоль поля со скоростью ; 2) равно­мерного движения со скоростью по окружности в плоскости, пер­пендикулярной полю. Радиус окружности определяется формулой (1). В результате сложения обоих движений возникает движение по спирали, ось кото­рой параллельна магнитному полю (рис. 1). Шаг винтовой линии

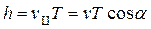
Подставив в последнее выражение (2), получим

.

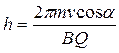Направление, в котором закручивается спираль, зависит от знака заряда ча­стицы.

Не нашли, что искали? Воспользуйтесь поиском: