Вариационные ряды и их графическое представление

Установление статистических закономерностей, присущих случайным массовым явлениям, основано на изучении статистических данных- сведений о том, какие значения принял в результате наблюдений интересующий нас признак (случайная величина Х).*

Расположение выборочных значений случайной величины в порядке неубывания называется ранжированием.

Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантой, а изменение этого значения - варьированием.

Численность отдельной группы сгруппированного ряда наблюдаемых данных называется частотой или весом варианты. Если i-индекс варианты, то – число измеренных значений i-той варианты.

Отношение к общей сумме частот всех вариант называется относительной частотой варианты и обозначается

=

Накопленной частотой варианте называется общее число вариант, имеющих значения признака, меньше или равные данному, то есть

X

Различают дискретные вариационные ряды и интервальные.

Дискретным вариационным рядом распределения (распределениям частот) называется ранжированная совокупность вариант с соответствующими им частотами или относительными частотами.

Интервальным вариационным рядом (интервальным распределением частот) называется упорядоченная последовательность интервалов варьирования случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений случайной величины.

Для выбора оптимальной величины интервала применяют формулу Стерджесса:

h= ,

где –максимальная варианта выборки; -минимальная варианта выборки; -объем выборки.

Величина R= называется размахом варианты или размахом вариационного ряда.

Величина N= –число классов.

Вариационные ряды графически могут быть изображены в виде полигона и гистограммы. Графическое изображение ряда распределения позволяет наиболее просто, наглядно отразить основную тенденцию вариации признаков.

Гистограмма используется для графического и представления распределений непрерывно варьирующих признаков и состоит из примыкающих друг к другу прямоугольников. Основание каждого прямоугольника равно ширине интервала класса, а высота его такова, что площадь прямоугольника пропорционально частоте попаданий в данный интервал.

Полигон частот образуется ломаной линией, соединяющей точки срединным значениям интервалов классов и частотами этих интервалов.

При составлении выводов по построенным графикам гистограммы и полигона об однородности выборки по заданному признаку, учитывают следующие моменты:

1. Если гистограмма и полигон по своему виду близки к виду графика нормального распределения, то группа однородна.

2. Если графики низкие и растянутые, то группа возможно, однородна, но некомпактна.

3. Если графики имеют 2 и более вершины, то группа неоднородна по данному признаку, ее необходимо разбить на подгруппы.

Пример 1. Определить однородность группы из 10 исследуемых в результатах прыжка в длину с места с помощью построения графиков вариационных рядов, если данные выборки таковы:

, см ~ 260; 255; 240; 250; 250; 264; 250; 262; 252; 258. (n=10)

Решение.

1.Проранжируем данный вариационный ряд в порядке неубывания:

, см ~ 240; 250; 250; 250; 2534 255; 258; 360; 262; 264.

2.Расчитаем размах вариационного ряда:

R=264-240=24(см).

3.Расчитаем число классов:

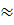N=1+lqn=1+3,32 1=4,32 5

4.Расчитаем интервал классов по формуле:

h= = см

5.Для графического представления данных вариационного ряда построим рабочую таблицу и произведем необходимые расчеты:

№ класса	Границы классов	Среднее значение классов	Частота класса	Накопленная частота
	240-245	242,5
	245-250	247,5
	250-255	252,5
	255-260	257,5
	260-265	262,5

Где среднее значение классов = +

6.Построим графики гистограммы и полигона данного вариационного ряда и сделаем вывод.

Вывод: т.к. графики гистограммы и полигона имеют три вершины, то группа по результатам прыжка в длину с места неоднородна, в тренировочном процессе ее следует разделить на три подгруппы с каждой из которых вести занятия по индивидуальным планам.

3. Числовые характеристики выборки.

Не нашли, что искали? Воспользуйтесь поиском: