Аксиома силлогизма и ее следствия

Если изобразить отношения между терминами нашего примера кругами, то у нас получится следующая схема.

На основе приведенной схемы можно сформулировать такое положение: Если объем одного термина (S) полностью входит в объем другого термина (М), а объем другого термина (М) полностью входит в объем третьего термина (р), то и объем первого термина (S) полностью входит в объем третьего термина (р). Это положение назы­вается аксиомой простого категорического силлогизма.

Из аксиомы силло­гизма можно вывести некоторые выводы, которые описывают ситуации, на­личие которых обеспечивает необходимый характер выводов из зафиксированных в посылках отношении между объемами имен.

С1. Если меньший термин входит в средний, а средние несов­местимый с большим, то и меньший термин несовместим с большим.

На­пример, «Сплавы (м) не являются металлами (р), а бронза (S) - это сплав (м). следовательно, бронза (S) не является металлом

(Р)», Необходимый характер вывода проиллюстрирован на рис.24.

С2. Если больший термин входит в средний, а меньший несовместимый со средним, то он несовместимый и с большим.

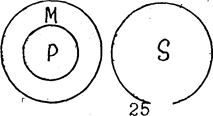
Например, «Все металлы (Р) электропроводны (М), а пластмасса (S) не является электропроводной (р), следовательно, пластмасса (S) не является металлом (Р)».

СЗ. Если средний термин входит в больший, а меньший термин только частично входит в средний, то меньший термин, по крайней мере, частично входит в больший (рис.26).

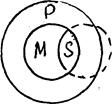
Например, «Все хищники (М) – кор­мятся мясом (р), а некоторые домашние животные (S) - хищники (М), следовательно, некоторые домашние животные (S) кормятся мясом (Р).

С4. Если большим термин входит в средний, а меньший частично вы­ключается из среднего, то он, по крайней мере, частично исключается из большего (рис.27).

Например, «Все вулканы (р) является горами (м), а некоторые источники подземного тепла (S) не являются горами (м). следовательно, некоторые ис­точники подземного тепла (S) не являются вулканами (р)».

Таковы следствия из аксиомы силлогизма. Описанные в них ситуации, обеспечивающие необходимый характер выво­дов, могут быть созданы при соответствии отношении, отраженных в посылках, некоторым логическим условиям, которые традиционно называют­ся общими правилами простого категорического силлогизма,

Не нашли, что искали? Воспользуйтесь поиском: