Главные линии плоскости

Главные линии плоскости – это прямые частного положения (линии уровня), принадлежащие плоскости, а также линии наибольшего наклона плоскости к плоскостям проекций.

1. Линии уровня

Горизонталь плоскости – прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций. Все горизонтали плоскости параллельны между собой и параллельны горизонтальному следу плоскости (рис. 61 ÷ 63). Горизонтальный след плоскости является частным случаем горизонтали (прямая, принадлежащая и данной плоскости и горизонтальной плоскости проекций H)– нулевая горизонталь.

y

Фронталь плоскости – прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций. Все фронтали плоскости параллельны между собой и параллельны фронтальному следу плоскости (рис. 64 ÷ 66). Фронтальный след плоскости является частным случаем фронтали (прямая, принадлежащая и данной плоскости и фронтальной плоскости проекций V) – нулевая фронталь.

Рис. 66

Профильная прямая плоскости – прямая, принадлежащая плоскости и параллельная профильной плоскости проекций. Все профильные прямые плоскости параллельны между собой и параллельны профильному следу плоскости (рис. 67, 68). Профильный след плоскости является частным случаем профильной прямой плоскости (прямая, принадлежащая и данной плоскости и профильной плоскости проекций W) – нулевая профильная прямая плоскости.

`

2. Линии, определяющие угол наклона плоскости к плоскостям проекций.

Угол наклона плоскости, к любой из плоскостей проекций является двугранным углом, ребром которого служит след плоскости с данной плоскостью проекций. Для того, чтобы определить его величину следует, из любой точки плоскости опустить перпендикуляр на след плоскости. Линейный угол между перпендикуляром и его проекцией на данную плоскость проекций равен величине искомого двугранного угла. Такой угол легко определяется из прямоугольного треугольника, который строится для определения действительной величины отрезка. Таким образом, для определения угла наклона плоскости к плоскости проекций достаточно, из любой точки плоскости опустить перпендикуляр на след плоскости или на линию уровня, и определить действительную величину этого перпендикуляра.

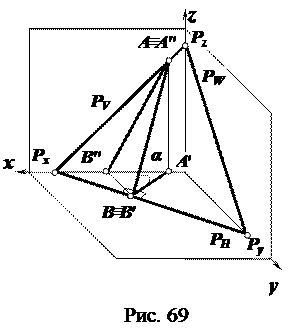
Линия ската – это прямая, принадлежащая плоскости и перпендикулярная горизонтальному следу плоскости (горизонтали плоскости), и определяющая угол наклона плоскости к горизонтальной плоскости проекций (рис. 69 ÷ 71). Для определения угла α наклона плоскости к горизонтальной плоскости проекций следует:

1) из любой точки плоскости провести линию ската (опустить перпендикуляр на горизонтальный след плоскости или на любую горизонталь плоскости);

2) найти основание этого перпендикуляра;

3) определить действительную величину перпендикуляра, построив прямоугольный треугольник действительных величин на его горизонтальной проекции;

4) угол этого треугольника, прилежащий к горизонтальной проекции линии ската, и будет равен углу наклона плоскости к плоскости проекций H.

Линия крутизны – это прямая, принадлежащая плоскости и перпендикулярная фронтальному следу плоскости (фронтали плоскости), и определяющая угол наклона плоскости к фронтальной плоскости проекций (рис. 72 ÷ 74).

Для определения угла β наклона плоскости к горизонтальной плоскости проекций следует:

1) из любой точки плоскости провести линию крутизны (опустить перпендикуляр на фронтальный след плоскости или на любую фронталь плоскости);

2) найти основание этого перпендикуляра;

3) определить его действительную величину, построив прямоугольный треугольник действительных величин на его фронтальной проекции;

4) угол этого треугольника, прилежащий к фронтальной проекции линии ската, и будет равен углу наклона плоскости к плоскости проекций V.

	Рис. 73

Линия, определяющая угол наклона плоскости к профильной плоскости проекций, собственного названия не имеет, однако – это прямая, принадлежащая плоскости и перпендикулярная профильному следу плоскости (профильной прямой плоскости).

Вопросы и задания для самопроверки

1. Какие признаки принадлежности прямой плоскости?

2. Определите, принадлежит ли точка M заданной плоскости (рис. 75, 76).

3. Какие прямые называются главными линиями плоскости?

4. В плоскостях, показанных на рис. 77 ÷84 проведите произвольные горизонталь и фронталь.

5. Достроить проекцию плоского многоугольника (рис. 85, 86).

Не нашли, что искали? Воспользуйтесь поиском: