Пересечение прямой с плоскостью общего положения

Для того, чтобы построить точку пересечения прямой с плоскостью (в общем случае) нужно:

1) через прямую провести вспомогательную плоскость (заключить прямую во вспомогательную плоскость), пересекающую данную плоскость удобным образом, т. е. линию пересечения которой с заданной плоскостью легко построить (чаще всего проводят проецирующую плоскость);

2) построить линию пересечения вспомогательной плоскости и данной;

3) определить на этой линии единственную точку принадлежащую заданной прямой;

4) если плоскость задана плоской фигурой, показать видимость.

Пример графического решения задачи показан на рис. 98, 99)

Рис. 98

Алгоритм решения задач для плоскости заданной не следами (рис. 100) такой же:

1) через прямую m провели вспомогательную фронтально-проецирующую плоскость Q (Q_V┴ ox), которая пересекла плоскость треугольника ABC по линии 1÷2 (собирательное свойство следа проецирующей плоскости);

2) на этой линии выбрали единственную точку K, принадлежащую прямой m;

3) видимость на горизонтальной проекции определена с помощью конкурирующих точек 3 и 4 (z₃ > z₄);

4) видимость на фронтальной проекции определена с помощью конкурирующих точек 2 и 5 (y₅ > y₂).

Пересечение плоскостей общего положения

Для построения линии пересечения плоскостей требуется определить две общие точки (точки, принадлежащие обеим плоскостям одновременно). Если хотя бы одна из плоскостей задана не следами, то алгоритм решения задачи следующий:

1. рассмотреть одну из плоскостей, как плоскость, а другую, как совокупность прямых;

6) найти точку пересечения одной из прямых с плоскостью,

7) операцию повторить;

8) соединить полученные точки, общие для обеих плоскостей прямой линией;

9) определить видимость.

Задача:

Найти линию пересечения плоскостей ABC и mn.

Решение (рис. 101)

1. Воспримем плоскость ABC, как плоскость, а плоскость mn, как совокупность прямых.

2. Найдем точку пересечения прямой m с плоскостью ABC. Для этого, проведем через прямую m вспомогательную фронтально-проецирующую плоскость P. Так как фронтальный след плоскости P_V обладает собирательным свойством, положение фронтальных проекций точек 1″ и 2″ пересечения сторон треугольника AB и BC, соответственно, плоскостью P, легко определяется. На горизонтальной проекции линии пересечения 1′2′ выберем точку K пересечения прямой m с плоскостью ABC.

3. Аналогично найдем точку пересечения прямой n с плоскостью ABC. Для этого, проведем через прямую n вспомогательную фронтально-проецирующую плоскость Q. Так как фронтальный след плоскости Q_V обладает собирательным свойством, положение фронтальных проекций точек 3″ и 4″ пересечения сторон треугольника AB и AC, соответственно, плоскостью Q, легко определяется. На горизонтальной проекции линии пересечения 3′4′ выберем точку D пересечения прямой n с плоскостью ABC. Линия пересечения плоскостей ABC и mn – это линия DK.

4. Видимость на фронтальной проекции определена с помощью конкурирующих точек 3 и 5 скрещивающихся прямых AB и n. Координата y точки 3, принадлежащей прямой AB, больше, чем у точки 5,принадлежащей прямой n (y₃ > y₅). Следовательно, точка 3 расположена ближе к наблюдателю, следовательно, в данном месте прямая n перекрывается плоскостью ABC, зачит плоскость mn видна правее линии пересечения KD.

5. Видимость на горизонтальной проекции определена с помощью конкурирующих точек 6 и 7 скрещивающихся прямых BC и n. Координата z точки 7, принадлежащей прямой BC, больше, чем у точки 6 (z₇ > z₆). Следовательно, точка 7 расположена выше и, следовательно, в данном месте прямая n закрыта плоскостью ABC, значит, видима часть плоскости mn левее линии пересечения KD.

В случае, когда описанный способ решения задачи по какой-либо причине неудобен (например, прямые, принадлежащие одной из плоскостей, пересекают другую плоскость вне пределов чертежа), возможен другой алгоритм решения.

Задача

Построить линию пересечения плоскостей, заданных треугольником ABC и параллельными прямыми m и n.

Решение (рис. 102)

Для построения линии пересечения плоскостей нужно найти две точки, общие для обеих плоскостей. Для их нахождения можно:

1) провести вспомогательную плоскость, пересекающую обе заданные плоскости по удобной линии (в данном случае проведена горизонтальная плоскость уровня P;

2) построить линии пересечения вспомогательной плоскости с обеими заданными (линии 1-2 и 3 - 4) плоскостями;

3) определить единственную точку общую для всех трех плоскостей (точка D – место пересечения линий 1 - 2 и 3 - 4);

4) операцию повторить. В данном случае проведена еще одна горизонтальная плоскость уровня Q. Построены линии пересечения с заданными плоскостями (линии 5 - 6 и 7 - 8). И определена единственная точка K общая для всех трех плоскостей;

5) линия DK и будет линией пересечения плоскостей ABC и mn.

Вопросы и задания для самопроверки

1. Назовите признак параллельности прямой и плоскости.

2. Каков стандартный алгоритм определения точки пересечения прямой с плоскостью.

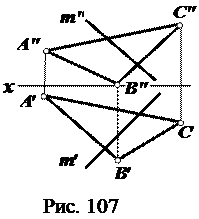
3. Определите точку пересечения прямой m и плоскости, покажите видимость (рис.103 ÷ 108).

5″ x		Рис. 105

4. Каков стандартный алгоритм определения линии пересечения плоскостей?

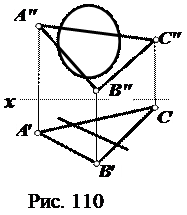
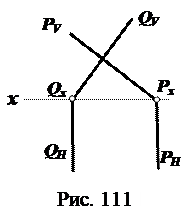
5. Определить линию пересечения плоскостей. В случаях задания плоскостей не следами показать видимость (рис. 109 ÷113).

Прямая перпендикулярная плоскости

Прямая, перпендикулярная плоскости является частным случаем пересечения прямой с плоскостью. Задачи на построение прямой, перпендикулярной плоскости можно разделить на две группы:

1) задачи, в которых из точки на плоскость нужно опустить перпендикуляр;

2) задачи, в которых необходимо из точки, принадлежащей плоскости, восставит к этой плоскости перпендикуляр.

Рассмотрим первый случай.

Задача.

Определить расстояние от точки M до плоскости P.

Решение (рис. 114÷116)

Алгоритм решения этой задачи следующий:

1) задать направление перпендикуляра. Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. Это значит, что в основании перпендикуляра (точке K) можно провести сколь угодно много пересекающихся прямых, принадлежащих плоскости P. И каждой из них отрезок MK будет перпендикулярен. Однако, прямой угол спроецируется на плоскости проекций без искажения только в том случае, если одна из его сторон будет параллельна плоскости проекций (теорема о проецировании прямого угла). Следовательно, в качестве таких пересекающихся прямых следует выбрать линии уровня плоскости, например, горизонталь и фронталь плоскости. Но не зная положения точки K – основания перпендикуляра – невозможно провести искомые прямые частного положения. Однако, поскольку все горизонтали плоскости (в том числе и горизонтальный след), параллельны между собой, горизонтальная проекция перпендикуляра M′K′ к плоскости будет перпендикулярна к горизонтальной проекции любой горизонтали плоскости, в том числе и горизонтальному следу (M′K′┴h′, M′K′┴P_H). А фронтальная проекция перпендикуляра M″K″, будет перпендикулярна фронтальной проекции любой фронтали плоскости, в том числе и фронтальному следу (M″K″┴f″, M″K″┴P_V). Таким образом, положение горизонтальной проекции перпендикуляра плоскости задается перпендикулярно проекции любой горизонтали плоскости, а фронтальной его проекции – перпендикулярно фронтальной проекции любой фронтали плоскости;

2) определить положение основания перпендикуляра точки K, как точки его пересечения с плоскостью (см. задачу о пересечении прямой и плоскости);

3) Определить действительную величину отрезка MK.

На рис. 116 приведен пример решения задачи для плоскости, заданной не следами.

Задачи, в которых необходимо из точки, принадлежащей плоскости, восставить к этой плоскости перпендикуляр, являются обратными рассмотреным выше. Их решение облегчается тем, что, как правило, известна точка основания перпендикуляра.

Зада ча

На расстоянии 30 мм от плоскости P провести плоскость ей параллельную.

Решение (рис. 117)

1. Выбрать точку, принадлежащую плоскости, – основание перпендикуляра. Для уменьшения количества дополнительных построений выберем точку A, расположенную на одном из следов плоскости (например, на фронтальном). Ее горизонтальная проекция будет располагаться на оси x.

2. Задать направление перпендикуляра. На горизонтальной проекции – перпендикулярно горизонтальной проекции любой горизонтали плоскости (в том числе и горизонтальному следу). На фронтальной проекции – перпендикулярно фронтальной проекции любой фронтали плоскости (в т.ч. и фронтальному следу).

3. На перпендикуляре отложить отрезок равный 30 мм. Для этого: ограничить луч произвольной точкой N, определить действительную величину отрезка AN методом прямоугольного треугольника, на гипотенузе построенного треугольника отложить отрезок равный 30 мм, затем, построить прямоугольный треугольник действительных величин, подобный, построенному для отрезка AN, Полученная точка B будет отстоять от плоскости P на расстояние равное 30 мм.

4. Через полученную точку B проведем плоскость параллельную данной, задав ее пересекающимися прямыми (прямая m // P_H, а прямая k // P_V).

Если плоскость задана не следами, то решение задачи не отличается от приведенного, но, ввиду отсутствия следов плоскости, требуется провести в заданной плоскости произвольные горизонталь и фронталь.

Задача

К плоскости треугольника ABC восставить перпендикуляр длиной 30 мм.

Решение (рис. 118)

1. Выберем точку, принадлежащую плоскости ABC, из которой будет восставлен перпендикуляр. Например, точку A.

2. Зададим направление перпендикуляра. Его горизонтальная проекция будет перпендикулярна горизонтальной проекции любой горизонтали плоскости (например – С1). А фронтальная проекция – перпендикулярна фронтальной проекции любой фронтали плоскости (например – A2).

3. Отложим на проведенном луче перпендикуляра отрезок равный заданному – 30 мм. Для этого установим принцип искажения величины любой из проекций по отношению к действительной величине отрезков на луче перпендикуляра. Этот принцип искажения зависит от угла наклона луча к любой из плоскостей проекций. Так как все отрезки, расположенные на луче имеют одинаковый угол наклона к любой из плоскостей проекций, определим этот угол для произвольно выбранного отрезка AN (ограничим луч произвольной точкой N). Методом прямоугольного треугольника определим действительную величинуотрезка AN, тем самым, установив угол наклона луча к плоскости проекций (в данном случае – H). Все отрезки, расположенные на луче перпендикуляра имеют одинаковый угол наклона к плоскости проекций, в том числе и отрезок AD длиной 30 мм. На гипотенузе треугольника действительных величин отложим отрезок равный 30 мм и построим прямоугольный треугольник, подобный, построенному для отрезка AN, тем самым, определив положение горизонтальной проекции точки N″.

Вопросы и задания для самопроверки

1. Каков стандартный алгоритм построения прямой, перпендикулярной плоскости?

2. Определите расстояние от точки M до плоскости. Покажите основание перпендикуляра, опущенного из точки M на плоскость (рис.119, 120).

3. Построить геометрическое место точек, удаленных от плоскости ABC на 30 мм (рис. 121).

Не нашли, что искали? Воспользуйтесь поиском: