МЕТОДЫ ПРЕОБРАЗОВАНИЯ ПРОЕКЦИЙ

Методы преобразования проекций – это способы решения сложных задач путем приведения их объектов к удобному (частному положению.

Существуют два основных типа методов преобразования проекций:

1) метод замены плоскостей проекций;

2) метод вращения.

При использовании второго метода, вращение может быть осуществлено:

1) вокруг осей перпендикулярных плоскостям проекций (иное название этого метода – метод вращения вокруг проецирующих прямых). Разновидностью этого метода является метод плоскопараллельного перемещения;

2) вокруг линий уровня. Разновидностью этого метода является метод вращения вокруг одного из следов плоскости (иное название – метод совмещения).

Ввиду краткости курса рассмотрим только два метода преобразования проекций: метод замены плоскостей проекций и метод вращения вокруг проецирующих прямых.

Метод замены плоскостей проекций

Сущность метода заключается в том, что объект проецирования остается неподвижным в пространстве, а вводится новая вспомогательная плоскость проекций (с сохранением правил ортогонального проецирования, то есть перпендикулярно одной из имеющихся плоскостей проекций) расположенная удобно (параллельно или перпендикулярно) по отношению к объекту.

Задача

Определить действительную величину отрезка AB.

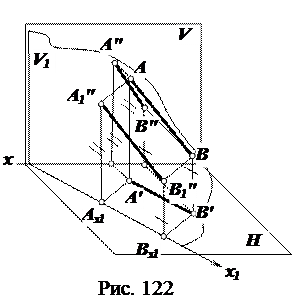
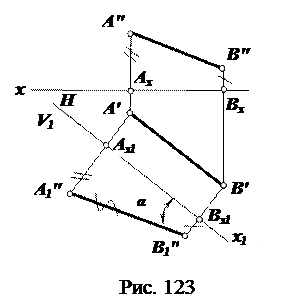
Решение (рис. 122, 123).

Отрезок проецировался бы без искажений, если бы был параллелен одной из плоскостей проекций. Поскольку отрезок AB не параллелен ни одной из плоскостей проекций проведем новую вспомогательную плоскость проекций (например V₁) перпендикулярно существующей плоскости проекций H и параллельно отрезку AB, то есть переведем его в частное положение – положение фронтали. Для этого воспользуемся одним из признаков фронтальной прямой – горизонтальная проекция фронтали параллельна оси x, т. е. новую ось x₁ проведем параллельно горизонтальной проекции A′B′. В соответствии с правилами ортогонального проецирования линии проекционной связи будут перпендикулярны оси x_{1 .} Так как при этом значения координат z для точек A и B не изменились, расстояние от старой фронтальной проекции A″ до старой оси x будет равно расстоянию от новой проекции A₁″ до новой оси x₁. Аналогично для точки B – B″B_x = B″B_x1. На новую плоскость проекций отрезок будет проецироваться в действительную величину. A″₁B″₁ = |AB |. При этом в действительную величину будет проецироваться и угол α наклона отрезка к плоскости проекций H.

Иногда однократной замены плоскостей проекций недостаточно. В этом случае операцию можно повторить, применив двух- трех- кратную замену. Рассмотрим это на примере задачи по расстояния от точки до прямой общего положения.

Задача

Определить расстояние от тоски C до прямой AB.

Решение (рис. 124).

Для того чтобы определить расстояние от точки до прямой, нужно опустить перпендикуляр из точки на прямую и узнать действительную величину получившегося отрезка. Задача решается просто, если прямая параллельна одной из плоскостей проекций. Тогда, по теореме о проецировании прямого угла, можно задать направление перпендикуляра и построить его основание. Однако прямая AB не является прямой частного положения. Но, также как в предыдущей задаче, можно перевести отрезок из общего положения в частное, и тогда задача сведется к уже известной, рассмотренной в разделе «Теорема о проецировании прямого угла». Для того чтобы определить действительную величину перпендикуляра CD можно ввести еще одну вспомогательную плоскость проекций, параллельную отрезку CD, например новую плоскость H₂. Тогда С′С_x1 = С′₂С_x2, а D′D_x1 = D′₂D_x2.

Использование метода замены плоскостей проекций значительно облегчает решение сложных задач связанных с взаимным положением прямой и плоскости, или нескольких плоскостей (задачи на перпендикуляр к плоскости, на пересечение плоскостей, на определение угла между плоскостями и т. п.). Такие задачи легко решаются, если плоскость находится в частном положении. Рассмотрим алгоритм перевода плоскости в проецирующее положение на примере задачи по нахождению натуральной формы плоской фигуры.

Задача

Определить натуральную форму треугольника ABC.

Решение (рис. 125)

Треугольник с проецируется на плоскость проекций без искажения, если будет этой плоскости параллелен. Значит нужно ввести новую плоскость проекций, параллельную плоскости треугольника. Но, сохраняя правила ортогонального проецирования, невозможно сразу ввести плоскость перпендикулярную одной из имеющихся плоскостей проекций и параллельную плоскости треугольника. В этом случае решение разбивают на два этапа:

1) вводят новую вспомогательную плоскость проекций перпендикулярную одной из имеющихся и перпендикулярно плоскости треугольника (переводят плоскость треугольника в проецирующее положение);

2) проводят плоскость параллельную плоскости треугольника.

Для реализации первого этапа – перевода плоскости в проецирующее положение – необходимо использовать признаки проецирующих плоскостей.

Для горизонтально-проецирующей плоскости определяющими признаками являются:

1) собирательное свойство горизонтального следа плоскости,

2) фронтальный след плоскости и фронтальная проекция любой фронтали плоскости перпендикулярна оси x.

Для фронтально-проецирующей плоскости определяющими признаками являются:

1) собирательное свойство фронтального следа плоскости,

2) горизонтальный след плоскости и горизонтальная проекция любой горизонтали плоскости перпендикулярна оси x.

Последовательной заменой плоскостей проекций переведем плоскость треугольника ABC в положение параллельной какой-либо из плоскостей проекций.

1. Введем вспомогательную плоскость проекций V₁ перпендикулярно плоскости треугольника. При этом новая ось x₁ должна быть перпендикулярна горизонтальной проекции любой горизонтали (например, A′1′). Признаком правильности проведенного построения будет то, что новые фронтальные проекции всех точек треугольника расположатся на одной прямой линии.

2. Введем новую плоскость проекций H₂ параллельно плоскости треугольника ABC. Для этого новую ось x₂ проведем параллельно новой фронтальной проекции A₁″B₁″C₁″. В результате на новую плоскость проекций H₂ треугольник ABC будет проецироваться без искажения.

Не нашли, что искали? Воспользуйтесь поиском: