Пересечение прямой с поверхностью геометрического тела

Общий принцип решения задач на построение точек пересечения прямой линии с поверхностью геометрического тела следующий:

1) через прямую провести вспомогательную плоскость, пересекающую поверхность геометрического тела по самой простой линии (дающей самую простую фигуру сечения – многоугольник, круг);

2) построить линию пересечения вспомогательной плоскости с поверхностью геометрического тела;

3) на этой линии определить точки общие для прямой и поверхности.

Задача

Построить точки пересечения прямой m с поверхностью пирамиды.

Решение (рис. 137)

1. Через прямую провести вспомогательную фронтально-проецирующую плоскость P.

2. Определить точки пересечения ребер пирамиды с вспомогательной плоскостью P (точки 1, 2, 3).

3. Построить треугольник 1 - 2 - 3 сечения поверхности пирамиды плоскостью P.

4. На линии 1 - 2 - 3 выбрать точки K и N общие для прямой m и поверхности пирамиды.

5. Показать видимость прямой m.

При решении задач по определению точек пересечения прямой с поверхностью тел вращения, следует помнить, какие же фигуры сечения могут получиться при пересечении стандартных геометрических тел различными плоскостями.

При пересечении цилиндра могут быть получены следующие виды сечений (рис. 138):

1. фигура конгруэнтная основанию (для кругового конуса это будет круг) – если секущая плоскость параллельна основанию;

2. прямоугольник – если секущая плоскость параллельна оси цилиндра;

3. эллипс – если секущая плоскость проходит под углом к оси цилиндра;

4. В случае, когда секущая плоскость, проходящая под углом к оси цилиндра, пересекает одно или два основания цилиндра, то в сечении получится фигура, ограниченная дугой (дугами) эллипса и прямой, или двумя прямыми, образовавшимися при пересечении плоскости и основанием (основаниями) цилиндра.

Естественно, что для решения задач наиболее подходят первый и второй случай, когда форма сечения или круг, или прямоугольник.

При пересечении конуса плоскостями могут быть получены следующие фигуры сечения (рис. 139):

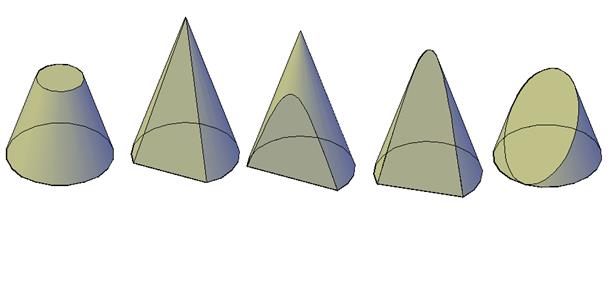
1. фигура подобная основанию (для кругового конуса – круг меньшего или большего диаметра) – если секущая плоскость параллельна основанию;

2. треугольник – если секущая плоскость проходит через вершину конуса;

3. фигура, ограниченная частью гиперболы и прямой, образовавшейся при пересечении плоскости и основания конуса – если плоскость параллельна оси конуса;

4. фигура, ограниченная частью параболы и прямой, образовавшейся при пересечении плоскости и основания конуса – если плоскость параллельна образующей конуса;

5. эллипс – если секущая плоскость расположена под углом к оси конуса и не параллельна образующей.

И для конуса наиболее подходящими являются первый и второй случай, когда форма сечения – круг и треугольник.

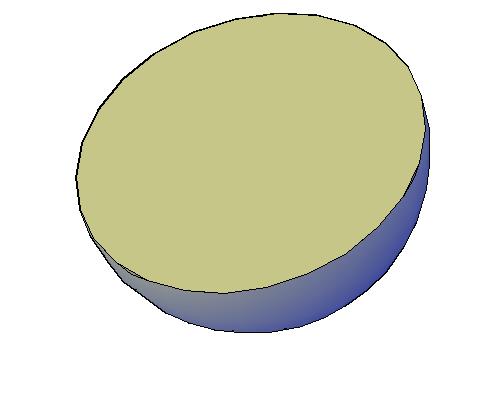
При пересечении шара любыми плоскостями, единственно возможным сечением является круг (рис. 140).

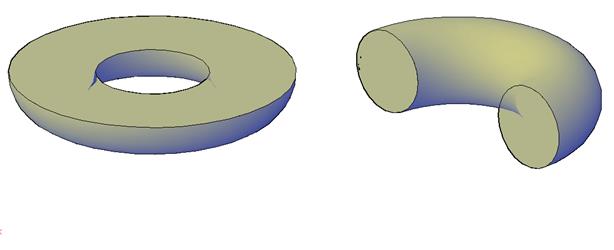
При пересечении тора плоскостями наиболее удобны случаи, когда в сечении получаются (рис.141):

1. кольцо – если секущая плоскость перпендикулярна оси тора;

2. две окружности – если секущая плоскость проходит через ось тора.

Во всех остальных случаях фигуры сечения сложны для построения.

Задача

Определить точки пересечения прямой m с поверхностью кругового конуса.

Решение (рис. 142)

1. Через прямую m провести вспомогательную плоскость P. Так как прямая m – горизонталь (это следует из того, что ее фронтальная проекция m″ параллельна оси x), разумно провести горизонтальную плоскость уровня.

2. Построить линию пересечения вспомогательной плоскости P с поверхностью конуса. Поскольку плоскость P параллельна основанию конуса, линией пересечения будет окружность с радиусом r, определяемым по построению.

3. На этой линии выбрать две точки (K и N), принадлежащих прямой m.

4. Определить видимость прямой.

Однако, не стоит каждый раз бездумно придерживаться схемы – через прямую проводить проецирующую плоскость. В каждом отдельном случае следует анализировать условие и, возможно, решение может быть упрощено.

Задача

Определить точки пересечения прямой m с поверхностью прямого кругового цилиндра.

Решение (рис. 143)

Очевидно, что проведение через прямую фронтально-проецирующей плоскости бессмысленно (фигурой сечения будет эллипс). Проведение горизонтально-проецирующей плоскости более разумно. Фигура сечения будет прямоугольником, на сторонах которого можно определить точки, принадлежащие прямой. Однако, поверхность цилиндра и так горизонтально-проецирующая, и горизонтальная проекция оснований будет обладать собирательным свойством. Следовательно, точки K и N пересечения горизонтальной проекции прямой и горизонтальной проекции цилиндра и будут точками пересечения прямой и поверхности цилиндра.

Несколько более сложны задачи, в которых проведение проецирующей плоскости не позволяет получить простую фигуру сечения. В этих случаях проводят вспомогательные плоскости общего положения, позволяющие получить простую фигуру сечения.

Задача

Построить точки пересечения прямой m с поверхностью прямого кругового конуса.

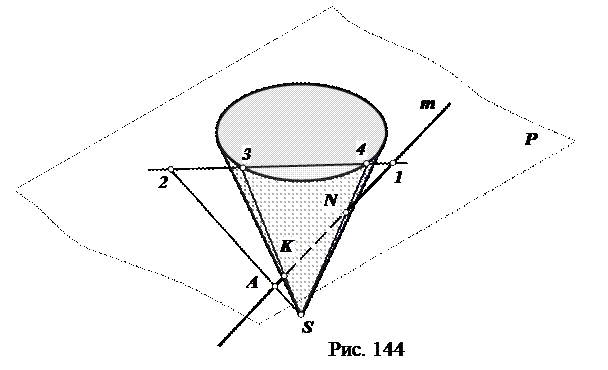
Решение (рис. 144 и 145)

Так как прямая m общего положения, а основание конуса параллельно горизонтальной плоскости проекций, невозможно через прямую провести плоскость, параллельную основанию конуса. Единственно приемлемым решением будет проведение плоскости, проходящей через прямую и вершину конуса. Такая плоскость пересечет поверхность конуса по треугольнику.

1. Провести вспомогательную плоскость, проходящую через вершину конуса и прямую m. Способ задания такой плоскости очевиден: прямая и не лежащая на ней точка (в данном случае – вершина конуса S).

2. Определить линию пересечения вспомогательной плоскости и плоскости основания конуса. Для этого определим две любые точки, принадлежащие обеим плоскостям. Одна из них – точка 1, принадлежащая прямой m, очевидна (плоскость P основания конуса – горизонтальная плоскость уровня, фронтальный след которой, обладает собирательным свойством. Для получения второй точки (точки 2), принадлежащей вспомогательной плоскости и плоскости P основания конуса, в пределах вспомогательной плоскости проведем любую прямую. Для этого на прямой m выберем произвольную точку A и проведем прямую SA, продлив ее до пересечения с плоскостью P основания конуса. Собирательное свойство следа горизонтальной плоскости основания конуса, позволит определить положение точки 2.

3. На линии 1-2 выбрать две точки 3 и 4, принадлежащие окружности основания конуса.

4. Линия 3 - S - 4 будет линией пересечения вспомогательной плоскости и поверхностью конуса. На ней следует определить точки K и N, принадлежащие прямой m.

5. Показать видимость прямой.

`

Задача

Определить точки пересечения прямой m с поверхностью наклонного цилиндра.

Решение (рис. 146, 147)

Эта задача похожа на предыдущую. И решение ее также сводится к проведению плоскости общего положения, дающей простую фигуру сечения.

1. Через прямую необходимо провести вспомогательную плоскость, дающую самую простую фигуру сечения. В данном случае, это плоскость параллельная оси цилиндра, которая пересечет поверхность цилиндра по прямоугольнику. Зададим эту плоскость двумя пересекающимися прямыми. Одной из этих прямых будет прямая m. Для проведения другой прямой выберем на прямой m произвольную точку A, и проведем через нее прямую n параллельную оси цилиндра.

2. Построим линию пересечения вспомогательной плоскости с плоскостью основания цилиндра. Ее положение будет определяться точками 1 и 2 пересечения прямых m и n с плоскостью основания цилиндра.

3. На полученной линии определим точки 3 и 4 ее пересечения с окружностью основания цилиндра.

4. Построим прямоугольник 3 – 4 – 5 - 6 сечения поверхности цилиндра вспомогательной плоскостью.

5. На контуре сечения выберем две точки C и D, принадлежащие прямой m.

6. Определим видимость прямой.

Принцип решения задач на нахождение точек пересечения прямой со сферой не отличается от вышеописанного. В этом случае также следует провести через прямую вспомогательную плоскость, дающую удобную фигуру сечения. Сечение шара любой плоскостью в любом случае – круг. Однако для того, чтобы увидеть натуральную форму сечения часто приходится прибегать к методам преобразования проекций.

Задача

Определить точки пересечения прямой AB с поверхностью шара.

Решение (рис. 148)

1. Проведем через прямую вспомогательную, в данном случае фронтально-проецирующую плоскость P.

2. Методом замены плоскостей проекций найдем натуральную форму сечения. Для этого проведем вспомогательную плоскость проекций H₁, параллельную плоскости P. При этом определится новая проекция центра шара S′₁. Проекция центра окружности сечения на плоскость H₁ будет совпадать с проекцией центра шара S′₁. Радиус окружности сечения R ясен из построения.

3. На линии окружности сечения выберем две точки K и M, принадлежащие заданной прямой.

4. Определим видимость прямой.

Не нашли, что искали? Воспользуйтесь поиском: