Пересечение поверхностей геометрических тел

При выполнении чертежей технических деталей часто возникает необходимость построения линий перехода, то есть проекций линий пересечения поверхностей различных частей детали. Как известно, каждую техническую деталь можно представить, как совокупность простейших геометрических тел (призм, пирамид, цилиндров, конусов, сфер). Построение линий перехода сводится к нахождению множества точек, принадлежащих поверхности обоих геометрических примитивов.

При построении линий перехода задача сводится к тому, чтобы найти совокупность точек, которые являются общими для обоих геометрических тел. Существуют различные способы достижения этой цели. Наиболее часто используются следующие:

1. Общий способ, при котором поверхности геометрических тел рассматриваются как совокупности различных поверхностей;

2. Способ, при котором поверхность одного геометрического тела рассматривается как совокупность поверхностей, а поверхность другого – как совокупность линий;

3. способ вспомогательных секущих плоскостей;

4. способ вспомогательных концентрических сфер;

5. способ полных сечений.

При необходимости можно использовать комплексные решения, сочетая элементы различных способов для решения конкретной задачи, включая применение методов преобразования проекций, для приведения объектов в удобное для построения положение.

Задача

Построить линию пересечения поверхностей прямой призмы и пирамиды с треугольным основанием.

Решение (рис. 159, 160)

В данном случае использован способ, при котором поверхность одного геометрического тела рассматривается как совокупность поверхностей, а поверхность другого – как совокупность линий.

Воспользовавшись тем, что боковая поверхность призмы профильно-проецирующая без дополнительных построений определим положение профильных проекций точек 5′″ и 3′″ пересечения ребра SB с гранями призмы mn и kn, точек 6′″ и 2′″ пересечения ребра SA с теми же гранями.

Для определения положения точек 1 и 4 пересечения профильно-проецирующего ребра n призмы с гранями соответственно ASC и BSC пирамиды, проведем через профильные проекции точек 1′″ и 4′″ прямую SD в пределах грани ASC и прямую SE в пределах грани BSC. Тогда на пересечении горизонтальных проекций S′D′ и S′E′ указанных прямых с горизонтальной проекцией ребра n′ определится положение точек соответственно 1′ и 4 ′.

Соединим полученные точки в последовательности 6 - 1 - 2 - 3 - 4 - 5 - 6. При этом на фронтальной проекции будет видимым участок 6 - 1 - 2, расположенный на передней грани ASC пирамиды. А на горизонтальной проекции видимым будет участок 1 - 6 - 5 - 4, расположенный на верхней грани mn призмы.

Рис. 159

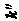
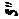
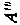
Задача

Построить линию пересечения поверхностей прямого кругового конуса и прямого кругового цилиндра.

Решение (рис. 161, 162)

Данную задачу можно решить несколькими способами. Например, воспользовавшись тем, что поверхность цилиндра профильно-проецирующая, провести по поверхности конуса ряд образующих, и затем найти точки пересечения образующих с проецирующей поверхностью цилиндра.

Однако в данном случае воспользуемся методом вспомогательных секущих плоскостей.

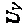
Профильная проекция линии пересечения совпадает с профильной проекцией цилиндра. Наметим на профильной проекции линии пересечения поверхностей ряд точек и построим их горизонтальные и фронтальные проекции.

Положения точек 1 и 16 пересечения крайней очерковой образующей конуса на профильной проекции определяются без дополнительных построений. Аналогично определяются точки 2, 3, 12, 13 пересечения крайних очерковых образующих конуса на фронтальной проекции с поверхностью цилиндра. Сначала построим их профильные, а затем фронтальные и горизонтальные проекции.

Для построения точек 4, 5, 6, 7, 8, 9, 10, 11, 14, 15 проведем несколько вспомогательных горизонтальных плоскостей P, Q, S, T, U.

Плоскость P пересекает поверхность конуса по окружности радиуса R_P. На пересечении горизонтальной проекции этой окружности и образующей цилиндра построим горизонтальные проекции точек 4′ и 5′. Положение фронтальных проекций этих точек 4″ и 5″ определится на фронтальном следе плоскости P_V, обладающем собирательными свойствами.

Плоскость Q пересекает поверхность конуса по окружности радиуса R_Q. На пересечении горизонтальной проекции этой окружности и образующей цилиндра построим горизонтальные проекции точек 6′ и 7′. Положение фронтальных проекций этих точек 6″ и 7″ определится на фронтальном следе плоскости Q_V, обладающем собирательными свойствами.

Плоскость S пересекает поверхность конуса по окружности радиуса R_S. На пересечении горизонтальной проекции этой окружности и образующей цилиндра построим горизонтальные проекции точек 8′ и 9′. Положение фронтальных проекций этих точек 8″ и 9″ определится на фронтальном следе плоскости S_{V ,} обладающем собирательными свойствами.

Плоскость T пересекает поверхность конуса по окружности радиуса R_T. На пересечении горизонтальной проекции этой окружности и образующей цилиндра построим горизонтальные проекции точек 10′ и 11′. Положение фронтальных проекций этих точек 10″ и 11″ определится на фронтальном следе плоскости T_V, обладающем собирательными свойствами.

Плоскость U пересекает поверхность конуса по окружности радиуса R_U. На пересечении горизонтальной проекции этой окружности и образующей цилиндра построим горизонтальные проекции точек 14′ и 1 5′. Положение фронтальных проекций этих точек 1 4″ и 1 5″ определится на фронтальном следе плоскости U_V, обладающем собирательными свойствами.

Соединим полученные точки в порядке 1-2-4-6-8-10-12-14-16-15-13-11-9-7-5-3-1. На этой линии видимым будет только участок 14-16-15, расположенный ближе к наблюдателю, чем крайние очерковые образующие на фронтальной проекции цилиндра. А на горизонтальной – участок 6-4-2-1-3-5-7, расположенный выше очерковой образующей цилиндра

Задача

Построить линию пересечения поверхностей двух прямых круговых конусов, оси которых пересекаются.

Решение (рис. 163, 164)

Так как основное решение задачи производится в данном случае только на двух проекциях, в целях достижения большей наглядности построение на профильной проекции не приводится.

Без дополнительных построений можно определить только положение проекций точек 1, 6, 11, и 15 пересечения крайних очерковых образующих вертикального и горизонтального конусов.

Рис. 163

Проведем вспомогательную горизонтальную плоскость P, проходящую через ось вращения горизонтального конуса. Эта плоскость пересекает поверхность вертикального конуса по окружности радиуса r_P. Точки 4, 8, 13 и 17, общие для горизонтальной проекции этой окружности и горизонтальных проекций очерковых образующих горизонтального конуса, также будут принадлежать линии пересечения поверхностей.

Однако больше никаких секущих плоскостей, дающих простые фигуры сечений с каждым конусом, провести не удастся. Однако можно воспользоваться методом вспомогательных сфер. Известно, что если центр шара расположен на оси тела вращения, то линией пересечения их поверхностей будет окружность.

Из точки пересечения осей конусов проведем вспомогательную сферу радиуса R₁. Она пересечет поверхность вертикального конуса по окружности радиуса r_v1, а поверхность горизонтального конуса – по окружности радиуса r_h1. На пересечении горизонтальных проекций этих окружностей определим положение горизонтальных проекций точек 2′ и 10′, принадлежащих линии пересечения поверхностей.

Из точки пересечения осей конусов проведем вспомогательную сферу радиуса R_{2 .} Она пересечет поверхность вертикального конуса по окружности радиуса r_v2, а поверхность горизонтального конуса – по окружности радиуса r_h2 и r_h4. На пересечении горизонтальных проекций этих окружностей определим положение горизонтальных проекций точек 3′ и 9′, 12′ и 18′, принадлежащих линии пересечения поверхностей.

Из точки пересечения осей конусов проведем вспомогательную сферу радиуса R_{3 .} она пересечет поверхность вертикального конуса по окружности радиуса r_v3, а поверхность горизонтального конуса - по окружности радиуса r_h3 и r_h5. На пересечении горизонтальных проекций этих окружностей определим положение горизонтальных проекций точек 5′ и 7′, 14′ и 16′, принадлежащих линии пересечения поверхностей.

Таким образом, при пересечении поверхностей этих конусов образуются две замкнутые пространственные кривые: 1-2-3-4-5-6-7-8-9-10-1 и 11-12-13-14-15-16-17-18-11. На фронтальной проекции участки кривых 1-10-9-8-7-6 и 11-12-13-14-15, заслоняя собой остальные части кривых, будут видимы. А на горизонтальной проекции будут видимы участки 4-5-6-7-8-9 и 13-14-15-16-17, расположенные на верхней части поверхности горизонтального конуса.

Вопросы и задания для самопроверки

1. Что называется геометрическим телом?

2. Какое геометрическое тело называется многогранником?

3. Какое геометрическое тело называется призмой?

4. Какая призма называется треугольной? четырехугольной?

5. какое геометрическое тело называется пирамидой?

6. Какая пирамида называется правильной?

7. Назовите признаки принадлежности точки и прямой поверхности геометрического тела?

8. Что называется телом вращения? Приведите примеры?

9. Как называется фигура, которая получается при пересечении поверхности геометрического тела плоскостью?

10. Какая фигура образуется при пересечении многогранника плоскостью?

11. Постройте сечение пирамиды плоскостью P (рис. 165). Определите натуральную форму сечения.

12. Перечислите возможные фигуры сечения цилиндра, конуса, шара, тора.

13. Каков стандартный алгоритм нахождения точек пересечения прямой с поверхностью геометрического тела?

14. Сколько вариантов решения задачи по нахождению точек пересечения прямой m с поверхностью прямого кругового конуса (рис. 166) Вы можете предложить?

15. Каков стандартный алгоритм построения линий пересечения поверхностей многогранников?

16. Какие способы построение линий пересечения поверхностей геометрических тел, одно из которых не является многогранником, Вы знаете?

17. Сколько способов построения линий пересечения поверхностей двух цилиндров (рис. 167) Вы можете предложить?

18. Построить три проекции деталей с отверстиями (на всех проекциях выполнить сочетание вида с разрезом:

а) шар с вертикальным коническим отверстием (рис. 167);

б) цилиндр с горизонтальным призматическим отверстием (рис.168);

в) шар с горизонтальным призматическим отверстием (рис.169).

19. Что называется разверткой поверхности?

20. Какие поверхности называются развертывемыми? приведите примеры.

21. Какие поверхности называются неразвертывемыми? приведите примеры.

22. Какие способы построения разверток поверхностей Вы знаете?

23. В чем заключается сущность метода триангуляции при построении разверток поверхностей?

24. Какие способы построения условных разверток поверхностей Вы знаете? В чем их сущность?

Не нашли, что искали? Воспользуйтесь поиском: