
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Метод вращения вокруг осей перпендикулярных плоскостям проекций
Сущность метода заключается в том, что плоскости проекций остаются неподвижными, а одна из точек объекта проецирования фиксируется осью перпендикулярной к одной из плоскостей проекций, и затем вращением вокруг этой оси, переводится в положение удобное для решения задачи (частное).
Задача
Определить действительную величину отрезка AB и угол его наклона к плоскости проекций H.
Решение (рис. 126)
Отрезок AB и угол α его наклона к горизонтальной плоскости проекцй были бы видны в без искажения, если бы отрезок был параллелен фронтальной плоскости проекций. Для решения задачи нужно перевести отрезок AB в положение фронтали. При этом на фронтальную плоскость без искажения будет проецироваться и сам отрезок, и угол наклона к горизонтальной плоскости проекций.
Порядок решения задачи, в данном случае следующий:
1) выбрать ось вращения перпендикулярную плоскости проекций H и проходящую через одну из точек отрезка (например, точку B);
2) вращать отрезок AB вокруг этой оси до тех пор, пока горизонтальная проекция отрезка A1′B1′ не станет параллельна оси x (признак фронтальной прямой). При этом горизонтальная проекция точки A′ будет двигаться по дуге окружности с радиусом равным величине проекции (A′B′). Поскольку при вращении координата z точки A не изменится, фронтальная проекция точки A″ будет двигаться по прямой параллельной оси x, до тех пор, пока не окажется на одной линии проекционной связи с горизонтальной проекцией A′.

Задача
Определить натуральную форму треугольника ABC.
Решение (рис. 127).
Треугольник будет проецироваться без искажений, если будет расположен параллельно одной из плоскостей проекций. В данном случае, треугольник расположен во фронтально-проецирующей плоскости (фронтальные проекции всех точек сошлись на одну прямую). Если зафиксировать одну из точек (например, точку B) осью, перпендикулярной фронтальной плоскости проекций и повернуть плоскую фигуру вокруг этой оси до положения плоскости уровня, то на горизонтальную плоскость треугольник спроецируется без искажения.

Иногда однократного поворота недостаточно. В этом случае операцию можно повторить, применив двух- трех- кратный поворот. Рассмотрим это на примере задачи по определению натуральной формы плоской фигуры.
Задача
Определить натуральную форму треугольника ABC.
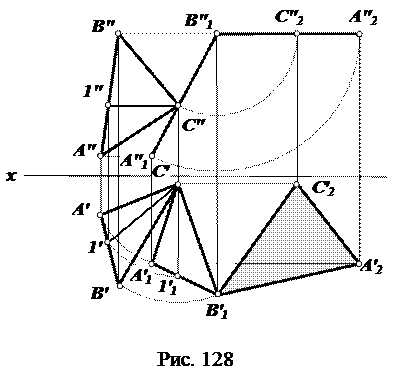
Решение (рис. 128)
Так же как и при использовании метода замены плоскостей проекций, решим задачу в два этапа:
1) переведем плоскость треугольника в проецирующее положение (для этого воспользуемся признаками проецирующих плоскостей);
2) будем вращать плоскую фигуру до положения плоскости уровня (см. предыдущую задачу).
Для этого используем следующий алгоритм решения:
1. Зафиксируем одну из точек плоскости треугольника (например, точку C) осью перпендикулярной одной из плоскостей проекции. В данном случае – осью перпендикулярной горизонтальной плоскости проекций.
2. Повернем треугольник вокруг этой оси до положения фронтально-проецирующей плоскости (переведем треугольник в частное фронтально-проецирующее положение). То есть после поворота фронтальные проекции всех точек треугольника должны расположиться вдоль одной прямой (собирательное свойство следа проецирующей плоскости). Так как угол наклона плоскости треугольника к горизонтальной плоскости проекций при повороте не меняется, форма горизонтальной проекции также не должна измениться. Должно измениться ее положение. Положение новой проекции треугольника можно определить, воспользовавшись свойствами проецирующей плоскости. А именно: горизонтальный след и горизонтальная проекция горизонтали фронтально-проецирующей плоскости перпендикулярны оси x. То есть новая горизонтальная проекция горизонтали C1′11′ станет перпендикулярна оси x. При этом горизонтальные проекции точек треугольника будут перемещаться по дугам окружностей. И величины проекций сторон не изменятся, т. е. задача сводится к школьному курсу – построению треугольника равного данному по трем сторонам при фиксированном положении одной из сторон.
3. Зафиксируем одну из точек плоскости треугольника (например, точку B) осью перпендикулярной одной из плоскостей проекции. В данном случае – осью перпендикулярной фронтальной плоскости проекций.
4. Повернем треугольник вокруг этой оси до достижения им положения плоскости уровня (в данном случае до положения горизонтальной плоскости). При этом на горизонтальную плоскость проекций треугольник ABC спроецируется без искажений.
Вопросы и задания для самопроверки
1. Для чего применяются методы преобразования проекций?
2. Какие методы преобразования проекций Вы знаете?
3. В чем сущность метода замены плоскостей проекций?
4. Какую новую вспомогательную плоскость нужно ввести для перевода отрезка в положение:
а) – фронтали,
б) – горизонтали,
в) – профильной прямой?
Как при этом должна располагаться новая ось?
5. Методом замены плоскостей проекций определите угол наклона отрезка AB (рис. 129) к:
а) – горизонтальной плоскости проекций,
б) – фронтальной плоскости проекций,
в) – профильной плоскости проекций.

6. Какую новую вспомогательную плоскость нужно ввести для перевода плоскости общего положения в:
а) – горизонтально-проецирующее положение,
б) – фронтально-проецирующее положение,
в) – профильно-проецирующее положение?
Как при этом должна располагаться новая ось?
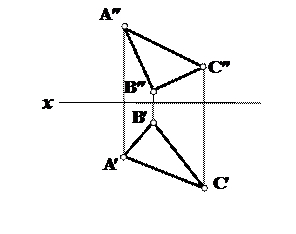
7. Методом замены плоскостей проекций определить угол наклона плоскости треугольника ABC к:
а) – горизонтальной плоскости проекций,
б) – фронтальной плоскости проекций,
в) – профильной плоскости проекций (рис. 130).
|
8. Методом замены плоскостей проекций определить расстояние от точки M до плоскости треугольника ABC (рис. 131).
|

9. Определить расстояние между параллельными прямыми AB и CD (рис. 32.

10. Определить расстояние между скрещивающимися прямыми AB и CD (рис. 133).
|

11. В чем сущность метода вращения вокруг осей перпендикулярных плоскостям проекций?
12. Какое иное название метода вращения вокруг осей перпендикулярных плоскостям проекций Вы знаете?
13. Методом вращения вокруг осей перпендикулярных плоскостям проекций определите действительные величины отрезков AB и AC (рис 134).

Не нашли, что искали? Воспользуйтесь поиском: