Потенциальная энергия - это функция, которая определяется с точностью до прибавления некоторой произвольной постоянной.

Это обстоятельство, однако, совершенно несущественно, ибо во все формулы входит только разность значений в двух положениях частицы. Поэтому произвольная постоянная, одинаковая для всех точек поля, выпадает. В связи с этим ее обычно опускают, что и сделано в трех предыдущих выражениях.

Потенциальную энергию следует относить не к частице, а к системе взаимодействующих между собой частицы и тел, вызывающих силовое поле. Определим поле сил по заданной потенциальной энергии как функции положения частицы в поле.

При перемещении частицы из одной точки потенциального поля в другую работа, которую производят силы поля, может быть представлена как убыль потенциальной энергии частицы, т. е. Это относится и к элементарному перемещению или

(8.14)

Учитывая, что , где - элементарный путь, перепишем уравнение (8.14) в форме

где - это убыль потенциальной энергии в направлении перемещения . Отсюда

(8.15)

Символ - частной производной - подчеркивает, что производная берется по определенному направлению.

Можно представить

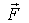где проекция вектора на орт а не на перемещение , как в случае

Подставив последнее выражение в уравнение (8.14), получим

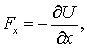
Для проекций и уравнения будут аналогичны уравнению для .

Итак

Величину, стоящую в скобках, называют градиентом скалярной функции U и обозначают или Значок "набла" означает символический векторный оператор

.

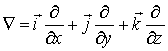Поэтому формально можно рассматривать как произведение символического вектора на скаляр .

Таким образом

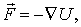
(8.16)

т. е. сила поля равна со знаком минус градиенту потенциальной энергии частицы в данной точке поля. Можно сказать и проще: сила поля F равна антиградиенту потенциальной энергии. Последняя формула дает возможность, зная функцию , восстановить поле сил .

Эквипотенциальная поверхность - поверхность, во всех точках которой потенциальная энергия U имеет одно и то же значение.

Из (8.15) следует, что проекция вектора на любое направление, касательное к эквипотенциальной поверхности в данной точке, равна нулю. Это значит, что вектор нормален эквипотенциальной поверхности в данной точке. Далее, возьмем перемещение в сторону уменьшения U, тогда U меньше 0, и, согласно (8.15), т.е. вектор направлен в сторону уменьшения U. А так как противоположен по направлению вектору , то мы приходим к выводу, что градиент U - это вектор, направленный по нормали к эквипотенциальной поверхности в сторону возрастания потенциальной энергии U.

Рис. 8.8. Эквипотенциальные поверхности и направление силы

В заключение заметим, что можно говорить о градиенте не только функции U, но и любой другой скалярной функции координат. Понятие градиента широко используется в самых различных разделах физики, особенно в теории электромагнетизма.

Рассмотрим понятие поля сил. Опыт показывает, что в случае гравитационных и электростатических взаимодействий сила , действующая на частицу А со стороны окружающих тел (системы В), пропорциональна массе (или заряду) частицы А Другими словами, сила может быть представлена в виде произведения двух величии:

,

(8.17)

Вектор называют напряженностью поля. Одно из важнейших свойств полей заключается в том, что поле, образованное несколькими источниками, равно сумме полей, созданных каждым из них. Точнее, напряженность результирующего поля в произвольной точке

(8.18)

где - напряженность поля соответствующего источника в этой же точке. Эта формула выражает так называемый принцип суперпозиции (или наложения) полей, который является отражением опытных фактов и дополняет законы механики.

Обратимся теперь к потенциальной энергии частицы. Формулу (8.14) можно записать так: Поделив обе части на т и обозначив получим

(8.19)

или

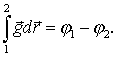
(8.20)

Функцию называют потенциалом поля в точке с радиус-вектором .

Потенциалы гравитационного ноля точечной массы т и кулоновского поля точечного заряда q определяются, согласно (8.12), формулами

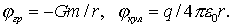
(8.21)

Заметим, что потенциал, как и потенциальная энергия, может быть определен только с точностью до прибавления некоторой произвольной постоянной, также совершенно несущественной. Поэтому ее обычно опускают, полагая равной нулю.

Итак, поле можно описывать или в векторном виде , или в скалярном . Практически же оказывается, что второй способ описания поля с помощью потенциала в большинстве случаев значительно удобнее. Этому есть несколько причин.

1. Зная , можно немедленно вычислить потенциальную энергию U и работу сил поля A:

(8.22)

2. Вместо трех компонент векторной функции проще задавать скалярную функцию .

3. Когда поле создается многими источниками, потенциал рассчитывать легче, чем вектор : потенциалы - скалярные величины, их можно просто складывать, не заботясь о напрвлении сил. Действительно, согласно (8.18) и (8.19), то есть

(8.23)

где потенциал, создаваемый 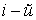частицей в данной точке поля.

4. И наконец, зная функцию , можно легко восстановить поле - как антиградиент потенциала :

(8.24)

Эта формула непосредственно следует из (8.16).

Не нашли, что искали? Воспользуйтесь поиском: