Закон сохранения полной механической энергии системы

Рассмотрим систему из двух частиц. Вычислим элементарную работу сил, с которыми эти частицы взаимодействуют между собой.

Согласно третьему закону Ньютона , поэтому

, и

.

Сила 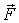- центральная, поэтому работа этой силы равна убыли потенциальной энергии взаимодействия данной пары частиц, т. е.

Так как функция 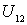зависит только от расстояния между частицами, то ясно, что работа не зависит от выбора системы отсчета.

Рассмотрим систему из трех частиц.

Но для каждой пары взаимодействий, как было показано , поэтому

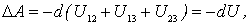
где функция есть собственная потенциальная энергия данной системы частиц:

Собственная потенциальная энергия U данной системы зависит от конфигурации системы.

Подобные рассуждения справедливы и для системы из любого числа частиц. Поэтому каждой конфигурации произвольной системы частиц присуща своя собственная потенциальная энергия U, и работа всех центральных внутренних сил при изменении конфигурации системы равна убыли собственной потенциальной энергии системы, т. е.

(8.35)

а при конечном перемещении всех частиц системы

(8.36)

где и -значения потенциальной энергии системы в начальном и конечном состояниях.

Собственная потенциальная энергия системы U - величина неаддитивная, т. е. она не равна в общем случае сумме собственных потенциальных энергий ее частей. Необходимо учесть еще потенциальную энергию взаимодействия отдельных частей системы

,

(8.37)

где - собственная потенциальная энергия части системы.

Следует также иметь в виду, что собственная потенциальная энергия системы, как и потенциальная энергия взаимодействия каждой пары частиц, определяется с точностью до прибавления произвольной постоянной, которая, впрочем, и здесь совершенно несущественна.

В заключение приведем полезные формулы для расчета собственной потенциальной энергии системы. Прежде всего покажем, что эта энергия может быть представлена как.

(8.38)

где - потенциальная энергия взаимодействия частицы со всеми остальными частицами системы. Здесь сумма берется по всем частицам системы.

Убедимся в справедливости этой формулы сначала для системы из трех частиц. Выше было показано, что собственная потенциальная энергия данной системы Преобразуем эту сумму следующим образом. Представим каждое слагаемое в симметричном виде: , ибо ясно, что . Тогда

Сгруппируем члены с одинаковым первым индексом:

Каждая сумма в круглых скобках представляет собой потенциальную энергию взаимодействия частицы с остальными двумя. Поэтому последнее выражение можно переписать так:

что полностью соответствует формуле (8.38).

Обобщение полученного результата на произвольную систему очевидно, ибо ясно, что подобные рассуждения совершенно не зависят от числа частиц, составляющих систему.

Для системы, взаимодействие между частицами которой носит гравитационный или кулоновский характер, формулу (8.38) можно преобразовать и к другому виду, воспользовавшись понятием потенциала. Заменим в (8.38) потенциальную энергию частицы выражением , где - масса (заряд) частицы, а - потенциал, создаваемый всеми остальными частицами системы в точке нахождения частицы.

Тогда

(8.39)

Если массы или заряды распределены в системе непрерывно, то суммирование сводится к интегрированию:

(8.40)

где -объемная плотность массы или заряда, 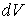-элемент объема. Здесь интегрирование проводится по всему объему, занимаемому массами или зарядами.

В качестве примера на применение последней формулы может служить задача, в которой необходимо провести расчет собственной потенциальной энергии гравитационного взаимодействия масс, распределенных по сфере и объему шара.

Не нашли, что искали? Воспользуйтесь поиском: