
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Лабораторная работа №3 Нахождение корней уравнения в MathCad
Цель работы: нахождение корней уравнения в программе MathCad с использованием встроенных функций root, polyroots, символьного решения.
Указания к выполнению лабораторной работы:
I Нахождение корней уравнения в программе MathCad с использованием встроенной функции root
1. Запустить программу MathCad.
2. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
3. Создать цикл из точек интервала, на котором определяются корни, и вычислить в этих точках функцию f(х). Построить график функции f(х) и график функции х0=0 (т.е. ось х).
4. Определить точки пересечения двух кривых f(х) и х0, которые будут приближением к корням уравнения.
4.1. Использовать для определения на графике значений корней в контекстном меню (рис.17, a) опцию Trace (рис. 17,б), установить флажок в окне Track Data Poіnt.
4.2. Подвести курсор мыши к точкам пересечения кривых, координаты точек пересечения кривых, т.е. корни, будут представлены в окнах Х-Value и У- Value, а на графике отобразится вертикальная прямая.
5. Задать для независимой переменной х начальное приближение, которое выбирается как значение точки пересечения кривых f(х) и х0. Обратиться ко встроенной в MathCad функции root(f(x), x) (функция root возвращает значение независимой переменной х, для которой f(х) равняется 0) и найти корень х1.
6. Найти второй (х2) и третий (х3) корни уравнения f(х)=0 (уравнение третьей степени имеет не больше трех действительных корней), задав для них соответственно их начальные значения как координаты точек пересечения кривых f(х) и х0 и использовав функцию root.


а) б)
Рисунок 17 – Диалоговые окна для определения координат точек пересечения кривых
ІІ Нахождение корней уравнения в программе MathCad с использованием встроенной функции polyroots, которая возвращает вектор, имеющий все корни уравнения, коэффициенты уравнения при этом задаются вектором.
1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
2. Записать как вектор v все коэффициенты уравнения, расположить их в порядке увеличения степеней.
3. Найти корни, обратившись ко встроенной функции r:=polyroots(v), результат будет получено относительно трансформированного вектора rT.
4. Для интервала нахождения корня и количества элементов вектора rT создать соответствующие циклы и вычислить значение функции в точках цикла.
5. Построить график функции в точках цикла, а также в найденных точках корней, в которых функция будет иметь значения, равные нулю.
ІІІ Нахождение корней уравнения в программе MathCad с использованием символьных решений уравнений.
1. Ввести левую часть уравнения.
2. Ввести знак равенства с использованием панели управления Evaluatіon (Выражения) или с помощью нажатия клавиш Ctrl + =.
3. За знаком равенства ввести правую часть уравнения.
4. Выделить переменную, относительно которой решается уравнение.
5. Выбрать команду Symbolіc/Varіable/Solve.
По окончанию решения корни уравнения выводятся в виде вектора.
ІV Найти приближенное решение с использованием функции mіnerr(x1,...).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения.
4. Обратиться к функции mіnerr(x). Корень будет найдено.
Таблица 1.1 – Варианты заданий к лабораторной работе № 1
| № варианта | Интервал нахождения корней | Уравнение |
| [-1; 3] | x3-2,92x2+1,4355x+0,791=0 | |
| [-2; 3] | x3-2,56x2-1,325x+4,395=0 | |
| [-3,5; 2,5] | x3+2,84x2-5,606x-14,766=0 | |
| [-2,5; 2,5] | x3+1,41x2-5,472x-7,38=0 |
Продолжение табл.1.1
| [-1,6; 1,1] | x3+0,85x2-0,432x+0,044=0 | ||
| [-1,6; 1,6] | x3-0,12x2-1,478x+0,192=0 | ||
| [-1,6; 0,8] | x3+0,77x2-0,251x-0,017=0 | ||
| [-1,4; 1] | x3+0,88x2-0,3999x-0,0376=0 | ||
| [-1,4; 2,5] | x3+0,78x2-0,827x-0,1467=0 | ||
| [-2,6; 1,4] | x3+2,28x2-1,9347x-3,90757=0 | ||
| [-2,6; 3,2] | x3-0,805x2-7x+2,77=0 | ||
| [-3; 3] | x3-0,345x2-5,569x+3,15=0 | ||
| [-2; 3,4] | x3-3,335x2-1,679x+8,05=0 | ||
| [-1; 2,8] | x3-2,5x2+0,0099x+0,517=0 | ||
| [-1,2; 3] | x3-3x2+0,569x+1,599=0 | ||
| [-2,5; 2,5] | x3-2,2x2+0,82x+0,23=0 | ||
| [-1,2; 4,6] | x3-5x2+0,903x+6,77=0 | ||
| [-1; 7,4] | x3-7,5x2+0,499x+4,12=0 | ||
| [-1.6; 9] | x3-7,8x2+0,899x+8,1=0 | ||
| [-3,4; 2] | x3+2x2-4,9x-3,22=0 | ||
| [-3,4; 1,2] | x3+3x2-0,939x-1,801=0 | ||
| [-4,6; 3,0] | x3+5,3x2+0,6799x-13,17=0 | ||
| [-2,4; 8,2] | x3-6,2x2-12,999x+11,1=0 | ||
| [-3,2; 2,7] | x3-0,34x2-4,339x-0,09=0 | ||
| [-1; 3] | x3-1,5x2+0,129x+0,07=0 | ||
| [-1; 3] | x3-5,5x2+2,79x+0,11=0 | ||
| [-1; 3] | x3-5,7x2-6,219x-2,03=0 | ||
| [-1; 3] | x3-3,78x2-7,459x-4,13=0 | ||
| [-1; 3] | x3-5x2-9,9119x+0,01=0 | ||
| [-1; 3] | x3-7x2-1,339x-7,55=0 |
Пример
І Для уравнения  найти корни на интервале [-1, 1], шаг изменения переменной х равен 0.1.
найти корни на интервале [-1, 1], шаг изменения переменной х равен 0.1.
1 Записать цикл из точек интервала х:=-1, -0.9..1.
2 Записать функцию х0 =0.
3 Построить графики для этих функций.
Примечание!
Первый способ
Для этого на панели "Graph" выберите "X-Y Plot" (самая первая из всех кнопок на панели), и тогда у вас на экране появится область построения графика. Для того, чтобы график в ней построился, нужно в центре под осью абсцисс написать имя нашей переменной (в данном случае им будет, конечно же, x), а по центру рядом с осью ординат — имя нашей функции (то есть f(x)).
Второй способ
1) нажимаешь комбинацию "shift+2". Появляется окно для построения графика
2)Справа задается сама функция. Например, надо построить у(х)=4х+5. Справа пишешь имя функции, т.е. "у(х)". Если надо в одних системах координат построить несколько графиков, то нажимаешь клавишу "Б" (только не забудь включить английский язык, MathCAD работает только с ним!),это действие переводит тебя на строку ниже и там вбиваешь вторую функцию. Так можно задавать намного больше функций.
3)снизу окна задается сама переменная, т.е. в нашем случае просто "х", если у второй функции переменная с другим именем, то вторую задаешь аналогичными действиями, как и в пункте 2.
4)щелкаешь мышью в пространство MathCAD и он строит тебе график с диапазоном по умолчанию. Если тебя диапазон не устраивает, то он указан вдоль осей, там его можно поменять.
P.S. если не знаешь, как задавать функцию, то для этого примера будет прямо в MathCAD'е выглядеть так:
у(х):=4х+5
4 Определить на графике точки пересечения кривых  и х0 =0.
и х0 =0.
Примечание!
Что ж, график у нас теперь есть. Как же определить, какая именно точка соответствует решению нашего уравнения? С этим поможет трассировка. Щелкните по получившемуся графику правой кнопкой мыши и выберите Trace. У вас на графике появится этакий "прицел", который можно будет передвигать мышкой, и окно, в котором будут отображаться координаты точки, находящейся в середине прицела (см. скриншоты).  Прицел этот можно, кстати, двигать и при помощи клавиатурных стрелочек, но все равно в любом случае передвигаться он будет исключительно и только вдоль кривой, отображающей ход нашей функции, нули которой мы и ищем. Думаю, основную идею вы уже уловили: передвигая крестик-"прицел" вдоль кривой, можно в окне трассировки увидеть точку, Y-координата которой будет равна нулю.
Прицел этот можно, кстати, двигать и при помощи клавиатурных стрелочек, но все равно в любом случае передвигаться он будет исключительно и только вдоль кривой, отображающей ход нашей функции, нули которой мы и ищем. Думаю, основную идею вы уже уловили: передвигая крестик-"прицел" вдоль кривой, можно в окне трассировки увидеть точку, Y-координата которой будет равна нулю.
Здесь, правда, может возникнуть небольшая проблема. В нашем уравнении, например, корень получился не целым, а трассировать функцию по X мы можем только с шагом, равным единице. Конечно, для того, чтобы локализовать корень для последующего применения функции root, в нашем случае достаточно и такой точности: достаточно найти интервал, на котором функция будет менять свой знак (то есть ее значение будет меняться с положительного на отрицательное или, напротив, с отрицательного на положительное). Но для других уравнений может случиться такое, что на единичном интервале может лежать и несколько решений — действительно, почему бы и нет, ведь даже для квадратных уравнений несложно придумать случай, когда такое может случиться. Какой из этого может быть выход? Самый простой и очевидный — уменьшить шаг трассировки по оси X, чтобы можно было более точно искать нулевые точки по оси Y. Сделать это в MathCAD очень просто. Помните, как мы задавали диапазон для нашей переменной x? Давайте кое-что поменяем и запишем его следующим образом: x:= -10,-9.9..10. Теперь уже шаг трассировки у нас будет не единица, а одна десятая (0,1). Для того, чтобы уменьшить его еще в десять раз, нужно записать x:= -10,-9.99..10. Общий принцип здесь вполне очевиден: мы записываем следующую точку диапазона следом за первой и, таким образом, указываем шаг, с которым MathCAD будет строить (а в итоге — и трассировать) наш график. Для более наглядного отображения данных имеет смысл добавить на график координатную сетку. Сделать это можно, если кликнуть по графику дважды, а затем в появившемся окне (см. скриншот) установить флажки напротив пунктов Grid Lines в категориях X Axis и Y Axis. Первый флажок устанавливает координатные линии для оси X, а второй, соответственно, для оси Y. Единственное, что также рекомендую — так это сразу поменять и цвет линий координатной сетки, кликнув по квадратикам рядом с этими пунктами — по умолчанию он задан кислотно-зеленым, что не очень удобно для глаз. Хотя это уже, конечно, дело вкуса.
5 Задать как приближение значения точек пересечения х1, х2, х3. В примере х1=-0.9, х2=0.2, х3= 0.7.
6 Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3). Полученные значения корней такие: х1=-0.92, х2=0.21, х3= 0.721 (рис. 18).

Рисунок 18 – Результат нахождения корней с использованием функции root
II Для уравнения 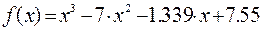 найти корни на интервале [-1.1, 7.1], шаг изменения переменной х равен 0.1.
найти корни на интервале [-1.1, 7.1], шаг изменения переменной х равен 0.1.
1. Создать вектор из коэффициентов уравнения, используя панель управления Matrix (Матрица) (рис.19) и задав один столбец и четыре строки для коэффициентов уравнения.

Рисунок 19 – Диалоговое окно для определения вектора из коэффициентов уравнения
Вектор из коэффициентов уравнения будет иметь следующий вид

2. С помощью встроенной функции r:= polyroots (v) найти корни уравнения и представить их в виде вектора rT, транспонированного по отношению к r, то есть преобразованного из столбца в строку.

3. Создать циклы для переменной х и количества найденных корней:

4. Построить графики для функции и определить функцию в точках корней. В точках корней значения функции равны нулю.
5. Определить значения корней на графике (рис. 20).
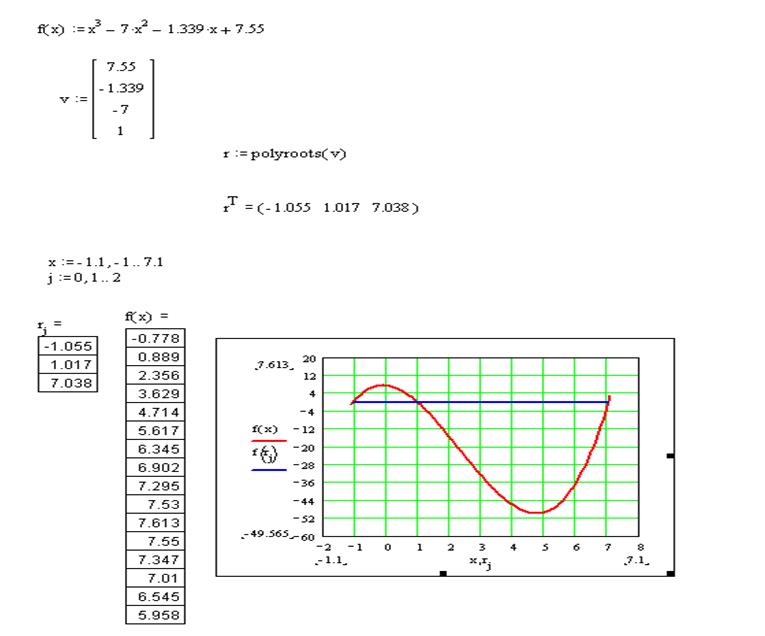
Рисунок 20 – Результат нахождения корней с использованием функции polyroots
III Для уравнения 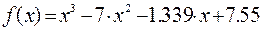 найти корни с использованием символьных решений уравнений.
найти корни с использованием символьных решений уравнений.
1. Записать левую часть уравнения
 .
.
2. Поставить логический знак «=» и в правой части записать 0.
Примечание!
В уравнениях нельзя использовать знак равенства, взятый с клавиатуры. Нужно использовать знак уравнения с панели инструментов (= или нажать одновременно Ctrl+ =).
3. Выделить переменную х.
4. Обратиться в главном меню MathCad к команде Symbolic/Variable/ Solve.
Найдены корни уравнения запишутся в виде вектора:

IV Найти приближенное решение вышеприведенного уравнения с использованием функции minerr (x 1,…).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово given (дано), с которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частью уравнения.
4. Обратиться к функции minerr (x). Корень будет найдено.
5. Аналогические действия выполнить для двух других корней уравнения, поскольку уравнения третьей степени имеет не больше трех корней.

Контрольные вопросы
1 Какие встроенные функции позволяют находить корни уравнения?
2 Как выполняется символьное нахождение корней уравнений?
Не нашли, что искали? Воспользуйтесь поиском: