
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Лабораторная работа №8 Вычисление производных в задачах геометрии и частных производных
Цель работы: вычисление производных в задачах геометрии и нахождение частных производных высоких порядков в программе MathCad.
Указания к выполнению лабораторной работы:
I Составить уравнение касательной и нормали к линии, которая задана уравнением y(x)=f(x) в точке М(x0,y0).
1 Задать значения х0 и у0 в точке М.
2 Записать уравнение линии у(х).
3 Определить производную от функции у(х) 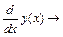 , использовав панель вычислений и панель символов. Присвоить значение производной функции уу(х): =
, использовав панель вычислений и панель символов. Присвоить значение производной функции уу(х): =  .
.
4. Записать уравнение касательной у виде
 ,
,
5. Аналогично записать уравнение нормали 
6. Построить графики касательной и нормали.
7 Отформатировать графики.
Таблица 6.1 – Варианты заданий к лабораторной работе
| Номер варианта | Функция f(x) для определения касательной и нормали | Точка М (х0,у0) для определения касательной и нормали | |||
| х2 -3х+5 | (2,3) | ||||
| х2 +2х+6 | (-1.1) | ||||
| х3-3х2 | (3,1) | ||||
| 0.5х-sin(x) | (0, p/3) | ||||
| (x-5)ex | (4,0) | ||||
| 1-(x-2)4/5 | (2,1) | ||||
| x5+5x-6 | (0,-1) | ||||
| (x3+4)/x2 | (2,3) | ||||
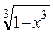
| (0,1) | ||||
| sin2(x) | (0.5,0.5) | ||||
| x2-0.5x4 | (0,0) | ||||
| х3-3х2 | (0, p/3) | ||||
| 0.5х-sin(x) | (4,0) | ||||
| (x-5)ex | (2,1) | ||||
| 1-(x-2)4/5 | (2,1) | ||||
| x5+5x-6 | (0,-1) | ||||
| 0.5х-sin(x) | (0, p/3) | ||||
| (x-5)ex | (4,0) | ||||
| 1-(x-2)4/5 | (2,1) | ||||
| x5+5x-6 | (0,-1) | ||||
| (x3+4)/x2 | (2,3) | ||||
| х3-3х2 | (3,1) | ||||
| 0.5х-sin(x) | (0, p/3) | ||||
| (x-5)ex | (4,0) | ||||
| 1-(x-2)4/5 | (2,1) | ||||
| x5+5x-6 | (0,-1) | ||||
| (x3+4)/x2 | (2,3) | ||||
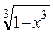
| (0,1) | ||||
| sin2(x) | (0.5,0.5) | ||||
| x2-0.5x4 | (0,0) | ||||
Пример
I Составить уравнение касательной и нормали к линии, которая задана уравнением y(x)=х4 -3х3+4х2-5х+1 в точке М(0,1).
1 Задать значения х0 и у0 в точке М: х0:=0, у0:=1.
2 Записать уравнения лини у(х):= х4 -3х3+4х2-5х+1.
3 Определить производную от функции у(х) 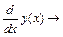 , использовав панель вычислений и панель символов. Присвоить значение производной функции уу(х): =
, использовав панель вычислений и панель символов. Присвоить значение производной функции уу(х): =  .
.
4 Записать уравнение касательной в виде
 ,
,
 . .
|
5 Аналогично записать уравнение нормали

|

|
6 Построить графики касательной и нормали.
7 Отформатировать графики.

|

|

|

|

|

|

|

|

|

|
Рисунок 24
График касательной и нормали
Контрольные вопросы
1 Як найти касательную к любой кривой в MathCad?
2 Як найти нормаль к любой кривой в MathCad?
3 Як выполнить символьные вычисления частных производных высокого порядка?
4 Як выполнить числовые вычисления частных производных высокого порядка?
Не нашли, что искали? Воспользуйтесь поиском: