Взаємодія точкових електричних зарядів

III. ЕЛЕКТРОСТАТИКА.

ПОСТIЙНИЙ ЕЛЕКТРИЧНИЙ СТРУМ

Взаємодія точкових електричних зарядів

Основні формули

1. Закон Кулона

,

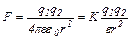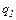де – сила взаємодії точкових за­рядів і , – відстань між за­рядами; – діелектрична проник­ність сере­довища; – електрична стала,

,

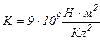2. Закон збереження еле­кт­ричного заряда 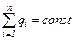, де – алгебраїчна сума зарядів, що входять в ізольо­вану систему, – число заря­дів.

Приклад розв'язання задачі

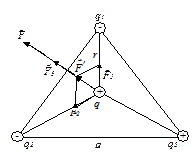
Приклад 1 У вершинах рівносторон­нього трикутника зі стороною 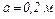знаходяться заряди 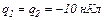і 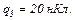У центрі трикутника поміщено заряд 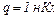. Визначити силу, що діє на заряд .

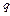Розв’язання

На заряд 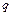діють три сили 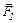, 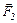і 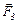. Оскільки заряди 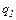і 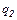рівні і знаходяться на одна­кових відстанях від заряду 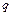, то

.

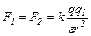Результуюча цих сил 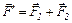і її значення

,

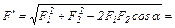
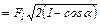де .

На заряд 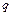діє і сила з бо­ку заряду 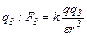. Сила 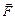, що діє на заряд 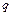, – це резуль­туюча сил 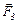і 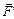, які напрямлені вздовж однієї прямої. Тому

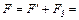
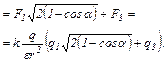
З рисунка видно, що

.

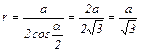Враховуючи, що

,

маємо .

Перевіримо одиниці вимірю­вання правої і лівої частини роз­рахункової формули

.

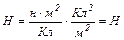Підставимо числові значення:

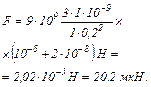
Приклад 2.

Відстань між двома точковими зарядами Q₁ = 2 нКл і
Q₂ =-3нКл, розташованими у вакуумі, дорівнює 20 см. Визначити: 1) напруженість Е; 2) потенціал φ поля, створюваного цими зарядами в точці, віддаленій від першого заряду на відстань r₁ = 15 см і від другого заряду на r₂ = 10 см.

Розв′язання:. Згідно принципу суперпозиції

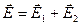(напрями векторів показані на рис.).

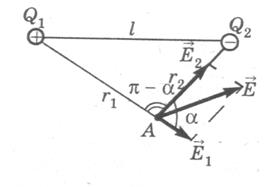
Напруженості електричного поля, створювані у вакуумі зарядами Q₁ і Q₂

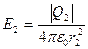E₁= , (1)

Модуль вектора Е знайдемо по теоремі косинусів:

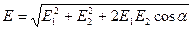(2)

де

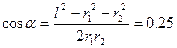(3)

Підставивши (1) і (3) у формулу (2), отримаємо шукану напруженість:

Е =

Згідно принципу суперпозиції, потенціал результуючого поля

φ = φ₁+φ₂, де

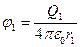і – потенціали полів, створюваних відповідно зарядами Qj і Q2.

Підставивши, знайдемо

.

Обчислюючи, одержуємо: 1) Е = 3 кВ/м; 2) φ = -150 В.

Задачі

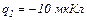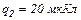18.1. Точкові заряди і знаходяться на відстані 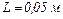один від одного. В точці, яка віддалена на відстані 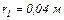від першого заряду і на від другого помістили третій заряд 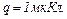Визначити силу , що діє на цей заряд.

18.2. Три однакові від’ємні заряди 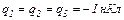розміщені у вершинах рівностороннього трикутника. Який за величиною додатний заряд 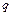треба помістити в центрі трикутника, щоб сила притягання з його боку врівноважила сили взаємного відштовхування зарядів, що знаходяться у вершинах.

18.3. У вершинах квадрата знаходяться однакові заряди 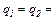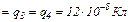. Який від’ємний заряд 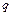треба помістити в центрі квадрата, щоб сили взаємного відштовхування додатних зарядів були зрівноважені силою притягання від’ємного заряду?

18.4. У вершинах правильного шестикутника зі стороною 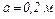розміщені точкові заряди 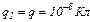, , , , , 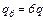. Знайти силу 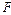, що діє на точковий заряд 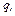що ле­жить в площині шестикутника і однаково віддалений від його вершин.

18.5. Чотири однакові заряди 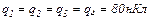закріплені у вершинах квадрата зі стороною 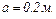Знайти силу , що діє на один із цих зарядів з боку решти трьох.

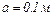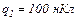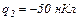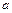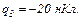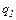18.6. На відстані знаходяться два точкових заряди і . На однаковій відстані від цих зарядів знаходиться заряд Визначити силу , що діє на цей заряд з боку зарядів і

18.7. Дві однакові провідні заряджені кулі знаходяться на відстані 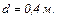Сила відштовхування куль дорівнює 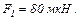Після того як кулі дотикнули одну до одної і розвели на попередню відстань, сила відштовхування зросла і стала дорівнювати 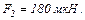Обчислити заряди 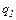і , які були на кулях до їх дотику. Діаметр куль вважати набагато меншим за відстань між ними.

18.8. Дві однакові провідні заряджені кулі знаходяться на відстані 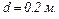Сила притягання куль 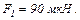Після того як кулі дотикнули одна до одної і розвели на попередню відстань, вони почали відштовхуватися з силою 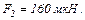Визначити заряди 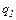і , які були на кулях до їх дотику. Діаметр куль вважати набагато меншим за відстань між кулями.

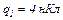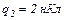18.9. Відстань між двома точковими зарядами і дорівнює 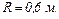На якій відстані від заряду 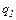треба по­містити заряд , щоб система знаходилась в рівновазі? Визначити величину заряду .

18.10. У вершинах правильного трикутника із стороною 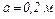знаходяться заряди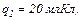 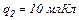і Визначити силу , що діє на заряд 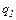з боку двох інших зарядів.

Не нашли, что искали? Воспользуйтесь поиском: