
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Закон Ома длЯ повного кола.ПотужнІсть струму
Основні формули
1. Сила постійного струму
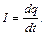
2. Густина електричного струму
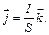
де 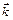 – одиничний вектор, який за напрямком збігається з напрямком руху додатних носіїв заряду,
– одиничний вектор, який за напрямком збігається з напрямком руху додатних носіїв заряду, 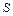 – площа поперечного перерізу провідника.
– площа поперечного перерізу провідника.
3. Опір однорідного провідника
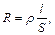
де r – питомий опір матеріалу провідника;  – його довжина;
– його довжина; 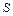 – площа поперечного перерізу провідника.
– площа поперечного перерізу провідника.
4. Закон Ома:
– для однорідної ділянки кола
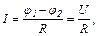
– для неоднорідної ділянки кола 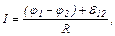
– для замкнутого кола
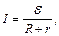
де 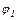 –
–  – різниця потенціалів на кінцях ділянки кола; e12 – ЕРС джерел струму, які входять у ділянку;
– різниця потенціалів на кінцях ділянки кола; e12 – ЕРС джерел струму, які входять у ділянку; 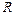 – опір зовнішнього кола;
– опір зовнішнього кола;  – внутрішній опір джерела; e – ЕРС усіх джерел у колі.
– внутрішній опір джерела; e – ЕРС усіх джерел у колі.
5. Робота, яку виконує електричне поле на ділянці кола постійного струму за час 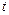 :
:
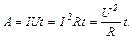
6. Потужність струму
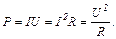
7. Повна потужність, яка виділяється в колі,
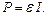
Приклад розв'язання задачі
При вмиканні електромотора в мережу з напругою 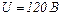 напруга на клемах розподільчого щита падає на
напруга на клемах розподільчого щита падає на  Опір підвідних проводів разом з опором електромотора
Опір підвідних проводів разом з опором електромотора 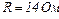 . Яку корисну потужність розвиває електромотор, якщо його ККД
. Яку корисну потужність розвиває електромотор, якщо його ККД 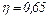 ?
?
Розв'язання
Під час роботи електромотора, ввімкненого в коло постійного струму, електрична енергія перетворюється в механічну і внутрішню енергію.
Якщо при вмиканні мотора по колу йде струм  , то згідно з законом збереження енергії за рахунок потужності
, то згідно з законом збереження енергії за рахунок потужності 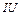 , що розвивається джерелом, відбувається нагрівання проводів
, що розвивається джерелом, відбувається нагрівання проводів 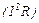 і розвивається механічна потужність
і розвивається механічна потужність 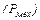 :
:
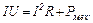
За рахунок механічної потужності долається тертя і виконується корисна робота. Якщо ККД електромотора h, то корисна потужність дорівнює:
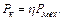
Напруга на клемах розподільчого щита при увімкненні мотора зменшується на  . Якщо розглядати ці клеми як затискачі джерела, то
. Якщо розглядати ці клеми як затискачі джерела, то
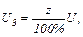
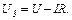
Звідси знайдемо силу струму  в колі,
в колі,
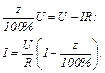
Підставимо отримані вирази у закон збереження енергії:
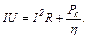
Звідси
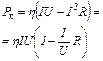
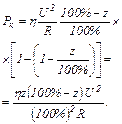
Підставимо числові значення:
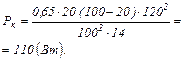
Задачі
23.1. ЕРС батареї 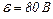 і її внутрішній опір
і її внутрішній опір 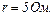 Зовнішнє коло споживає потужність
Зовнішнє коло споживає потужність  Визначити силу струму в колі і опір зовнішньої частини кола.
Визначити силу струму в колі і опір зовнішньої частини кола.
23.2. При зовнішньому опорі 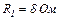 сила струму в колі
сила струму в колі  при опорі
при опорі  сила струму
сила струму 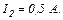 Визначити силу струму короткого замикання джерела ЕРС.
Визначити силу струму короткого замикання джерела ЕРС.
23.3. ЕРС батареї 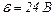 . Найбільша сила струму, яку може дати батарея,
. Найбільша сила струму, яку може дати батарея, 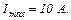 Визначити максимальну потужність, яка може виділятися у зовнішній частині кола.
Визначити максимальну потужність, яка може виділятися у зовнішній частині кола.
23.4. При вмиканні електромотора в мережу з напругою 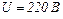 він споживає струм
він споживає струм  Визначити потужність, яка споживається мотором і його ККД, якщо опір обмотки мотора
Визначити потужність, яка споживається мотором і його ККД, якщо опір обмотки мотора 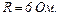
23.5. Низькоомна обмотка підмагнічування динаміка живиться від акумулятора з ЕРС 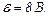 Лінія передачі має опір
Лінія передачі має опір  Яким повинен бути опір обмотки підмагнічування, щоб потужність струму підмагнічування в обмотці була
Яким повинен бути опір обмотки підмагнічування, щоб потужність струму підмагнічування в обмотці була  ?
?
23.6. Джерело напруги  живить коло, в яке ввімкнено електричну піч, з'єднану послідовно з опором
живить коло, в яке ввімкнено електричну піч, з'єднану послідовно з опором  Визначити опір печі, при якому її потужність дорівнюватиме
Визначити опір печі, при якому її потужність дорівнюватиме 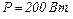
23.7. Генератор з ЕРС  і внутрішнім опором
і внутрішнім опором  виробляє струм
виробляє струм 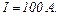 Зовнішній опір кола
Зовнішній опір кола  Визначити повну і корисну потужності генератора, електричні втрати і ККД. Скласти рівняння балансу потужностей.
Визначити повну і корисну потужності генератора, електричні втрати і ККД. Скласти рівняння балансу потужностей.
23.8. П'ять послідовно з'єднаних джерел ЕРС з внутрішнім опором  (кожний) замкнуто на зовнішній опір
(кожний) замкнуто на зовнішній опір 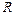 . Яким повинен бути опір R, щоб у зовнішньому колі виділялась максимальна потужність?
. Яким повинен бути опір R, щоб у зовнішньому колі виділялась максимальна потужність?
23.9. До двох батарей, які з'єднані паралельно, під'єднали електролампу. Яким повинен бути її опір, щоб потужність її була максимальною, якщо ЕРС батареї 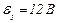 і
і  i їх внутрішній опір
i їх внутрішній опір 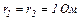 ?
?
23.10. При замиканні на провідник опором 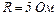 сила струму, яка створюється батареєю елементів, дорівнює
сила струму, яка створюється батареєю елементів, дорівнює 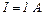 Сила струму короткого замикання батареї дорівнює
Сила струму короткого замикання батареї дорівнює 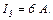 Яку найбільшу корисну потужність може забезпечити така батарея?
Яку найбільшу корисну потужність може забезпечити така батарея?
Закони КІрхгофа
Основні формули
1. Перший закон Кірхгофа: алгебраїчна сума струмів, які сходяться у вузлі, дорівнює нулю:
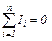
Струми, які входять у вузол, вважаються додатними, а які виходять з вузла – від'ємними.
2. Другий закон Кірхгофа: в замкненому контурі алгебраїчна сума спадів напруг на всіх ділянках контуру дорівнює алгебраїчній сумі ЕРС, які містяться в цьому контурі
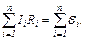
Якщо напрямок струму збігається з вибраним напрямом обходу контуру, то відповідний добуток сили струму на опір входить в рівняння із знаком "+", у протилежному випадку цей добуток входить із знаком "-". ЕРС беруть із знаком "+", якщо при обході контуру у вибраному напрямі перший електрод буде негативним, а другий – позитивним.
Приклад розв'язання задачі
Визначити силу струму, що проходить через опори 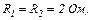
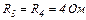 , увімкнені в коло, як показано на рисунку, якщо
, увімкнені в коло, як показано на рисунку, якщо 
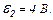 Опорами джерел струму можна знехтувати.
Опорами джерел струму можна знехтувати.
Розв'язання
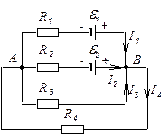
Щоб визначити сили струмів, застосуємо закони Кірхгофа. Виберемо довільно напрямки струмів у кожній ділянці кола.
Напрямок обходу контурів виберемо довільно – за годинниковою стрілкою.
За першим законом Кірхгофа для вузла В маємо:
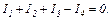
Запишемо другий закон Кірхгофа для контуру AR1BR2A:
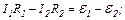
для контура AR1BR3A:
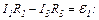
для контура AR3BR4A:
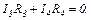
Підставимо в ці рівняння числові значення опорів і ЕРС:
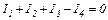
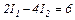
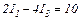
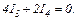
Розв'яжемо цю систему методом Крамера.
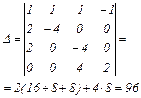
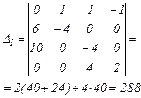
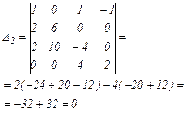
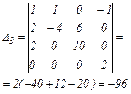
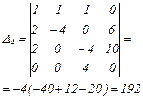
Отже,
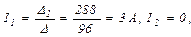
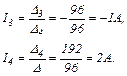
Знак "-" у числовому значенні струму  свідчить про те, що, вибираючи довільно напрямки струмів, ми помилилися: насправді струм
свідчить про те, що, вибираючи довільно напрямки струмів, ми помилилися: насправді струм  йде від вузла В до вузла А.
йде від вузла В до вузла А.
Задачі
| 24.1. | ЕРС елементів 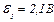 і і 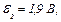 опори резисторів опори резисторів 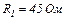 , ,  i i 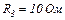 (див. рисунок). Знайти покази амперметра. Внутрішніми опорами елементів і опором амперметра знехтувати. (див. рисунок). Знайти покази амперметра. Внутрішніми опорами елементів і опором амперметра знехтувати.
| 
|
| 24.2. | ЕРС елементів 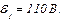 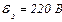 опори резисторів опори резисторів 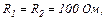  (див. рисунок). Визначити покази амперметра. Внутрішнім опором джерел і амперметра знехтувати. (див. рисунок). Визначити покази амперметра. Внутрішнім опором джерел і амперметра знехтувати.
| 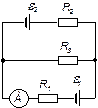
|
| 24.3. | ЕРС елемента 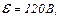 опори резисторів опори резисторів  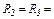 = 100 Ом (див. рисунок). Знайти потужність, що виділяється на резисторі = 100 Ом (див. рисунок). Знайти потужність, що виділяється на резисторі 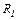 . Опором джерела струму знехтувати. . Опором джерела струму знехтувати.
| 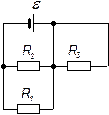
|
| 24.4. | ЕРС елементів  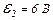 i i 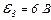 опори резисторів опори резисторів   і і  (див. рисунок). Знайти покази амперметра. Опором джерел струму знехтувати. (див. рисунок). Знайти покази амперметра. Опором джерел струму знехтувати.
| 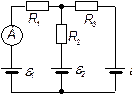
|
| 24.5. | Опір резисторів 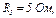  і і 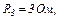 ЕРС джерела ЕРС джерела 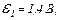 сила струму, який проходить через резистор сила струму, який проходить через резистор 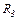 , ,  (див. рисунок). Знайти ЕРС (див. рисунок). Знайти ЕРС 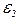 . Опором джерел струму знехтувати. . Опором джерел струму знехтувати.
| 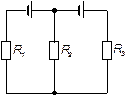
|
| 24.6. | ЕРС елементів  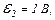 опір резисторів опір резисторів 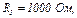 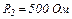 і і 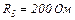 (див. рисунок). Знайти покази амперметра. Внутрішнім опором джерел струму і опором амперметра знехтувати. (див. рисунок). Знайти покази амперметра. Внутрішнім опором джерел струму і опором амперметра знехтувати.
| 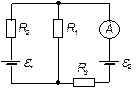
|
| 24.7. | ЕРС джерел струму 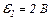 і і 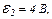 опори резисторів опори резисторів  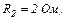 і і  (див. рисунок). Знайти покази амперметра. Внутрішнім опором елементів і амперметра знехтувати. (див. рисунок). Знайти покази амперметра. Внутрішнім опором елементів і амперметра знехтувати.
| 
|
| 24.8. | Опори резисторів 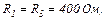 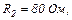 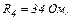 ЕРС джерела струму ЕРС джерела струму 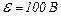 (див. рисунок). Знайти покази амперметра. Внутрішнім опором джерела і амперметра знехтувати. (див. рисунок). Знайти покази амперметра. Внутрішнім опором джерела і амперметра знехтувати.
| 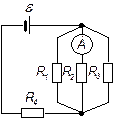
|
| 24.9. | ЕРС елементів 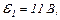  і і 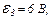 опори резисторів опори резисторів 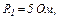  і і 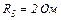 (див. рисунок). Знайти покази амперметра. Внутрішнім опором елементів і амперметра знехтувати. (див. рисунок). Знайти покази амперметра. Внутрішнім опором елементів і амперметра знехтувати.
| 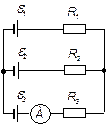
|
| 24.10.. | ЕРС елементів  їх внутрішні опори їх внутрішні опори 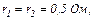 опори резисторів опори резисторів 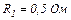 і і  (див. рисунок). Знайти покази амперметра. Опором амперметра знехтувати. (див. рисунок). Знайти покази амперметра. Опором амперметра знехтувати.
| 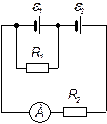
|
Теплова дІЯ струму
Основні формули
1. Закон Джоуля-Ленца для постійного струму
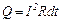 ,
,
де 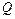 – кількість теплоти, яка виділяється в опорі
– кількість теплоти, яка виділяється в опорі  ділянки кола за час
ділянки кола за час 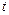 .
.
2. Якщо сила струму в провіднику змінюється, то закон Джоуля-Ленца справедливий для нескінченно малого інтервалу часу:
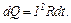
Приклад розв'язання задачі
Сила струму в провіднику опором 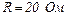 наростає протягом часу
наростає протягом часу  за лінійним законом від
за лінійним законом від 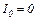 до
до  Визначити кількість теплоти, яка виділилась в цьому провіднику за першу секунду і за другу секунду.
Визначити кількість теплоти, яка виділилась в цьому провіднику за першу секунду і за другу секунду.
Розв'язання
Закон Джоуля-Ленца у вигляді  справедливий для постійного струму. Якщо ж сила струму в провіднику змінюється, то вказаний закон справедливий для нескінченно малого інтервалу часу і
справедливий для постійного струму. Якщо ж сила струму в провіднику змінюється, то вказаний закон справедливий для нескінченно малого інтервалу часу і
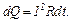
В даній задачі сила струму є функцією часу 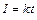 , де
, де 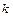 – коефіцієнт, що характеризує швидкість зміни сили струму:
– коефіцієнт, що характеризує швидкість зміни сили струму:
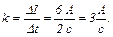
Тоді
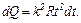
Проінтегруємо цей вираз в межах від 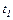 до
до  .
.
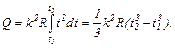
Проведемо обчислення:
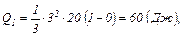
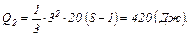
Задачі
25.1. За час 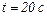 сила струму в провіднику опором
сила струму в провіднику опором 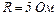 рівномірно зросла від нуля до деякого значення і при цьому виділилась кількість теплоти
рівномірно зросла від нуля до деякого значення і при цьому виділилась кількість теплоти 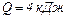 . Знайти швидкість збільшення сили струму.
. Знайти швидкість збільшення сили струму.
25.2. Сила струму в провіднику змінюється з часом за законом 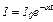 , де
, де 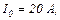
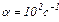 . Визначити кількість теплоти, що виділяється у провіднику опором
. Визначити кількість теплоти, що виділяється у провіднику опором 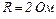 за час
за час 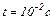 .
.
25.3. У провіднику за час  при рівномірному зростанні сили струму від
при рівномірному зростанні сили струму від 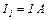 до
до 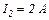 виділилась кількість теплоти
виділилась кількість теплоти 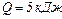 . Знайти опір провідника.
. Знайти опір провідника.
25.4. Сила струму в провіднику опором 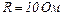 за час
за час 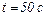 рівномірно зростає від
рівномірно зростає від 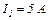 до
до  Визначити кількість теплоти
Визначити кількість теплоти 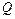 , що виділиться за цей час у провіднику.
, що виділиться за цей час у провіднику.
25.5. Сила струму в провіднику змінюється з часом за законом  . Знайти заряд, що проходить через поперечний переріз провідника за час t, що дорівнює половині періоду
. Знайти заряд, що проходить через поперечний переріз провідника за час t, що дорівнює половині періоду  , якщо початкова сила струму
, якщо початкова сила струму 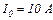 , циклічна частота
, циклічна частота  .
.
25.6. Сила струму в провіднику опором 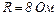 рівномірно зростає. За час
рівномірно зростає. За час  в провіднику виділилась кількість теплоти
в провіднику виділилась кількість теплоти  . Визначити заряд, що проходить у провіднику, якщо сила струму в початковий момент часу дорівнює нулю.
. Визначити заряд, що проходить у провіднику, якщо сила струму в початковий момент часу дорівнює нулю.
25.7. У провіднику опором 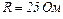 рівномірно зростає сила струму від нуля до деякого значення за час
рівномірно зростає сила струму від нуля до деякого значення за час 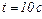 . Визначити середню силу струму, якщо у провіднику виділилась кількість теплоти
. Визначити середню силу струму, якщо у провіднику виділилась кількість теплоти 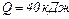 .
.
25.8. Визначити кількість теплоти, що виділилась за час  у провіднику опором
у провіднику опором 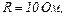 якщо сила струму у ньому, рівномірно зменшуючись, змінилась від
якщо сила струму у ньому, рівномірно зменшуючись, змінилась від 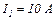 до
до 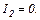
25.9. Сила струму в колі змінюється за законом  Визначити кількість теплоти, яка виділиться в провіднику опором
Визначити кількість теплоти, яка виділиться в провіднику опором 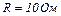 за час, що дорівнює чверті періоду (від
за час, що дорівнює чверті періоду (від  до
до 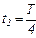 , де
, де 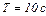 ).
).
25.10. Сила струму в колі змінюється з часом за законом  , де
, де  Визначити кількість теплоти, яка виділиться в провіднику опором
Визначити кількість теплоти, яка виділиться в провіднику опором 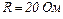 за час, протягом якого струм зменшиться вдвічі.
за час, протягом якого струм зменшиться вдвічі.
Не нашли, что искали? Воспользуйтесь поиском: