Розрахунок напруженості електричного поля

Основні формули

1. Напруженість електрично­го поля

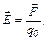
де 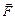– сила, з якою поле діє на внесений в дану точку пробний додатний заряд .

2. Напруженість поля, ство­реного точковим зарядом 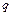на відстані r від нього,

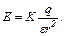
3. Напруженість поля, ство­рюваного рівномірно розподіле­ним зарядом вздовж тонкого стрижня,

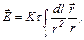
де 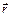– радіус-вектор, що спря­мований від виділеного елемента до точки, в якій визначається напруженість.

4. Потік вектора напруже­ності 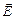через поверхню :

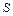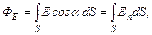
де 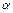– кут між вектором напруже­ності 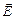і нормаллю 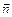до еле­мента поверхні; 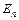– проекція вектора напруженості на нормаль.

5. Потік вектора напруже­ності 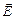через замкнену поверх­ню

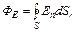
де інтегрування ведеться по всій поверхні.

6. Теорема Остроградського-Гаусса. Потік вектора 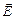через довільну замкнену поверхню до­рівнює алгебраїчній сумі зарядів, охоплених цією поверхнею, поді­леній на e₀:

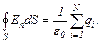
7. Напруженість поля, яке створюється нескінченно довгою рівномірно зарядженою ниткою на відстані від її осі:

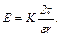
8. Напруженість поля, яке створене нескінченною рівномір­но зарядженою площиною

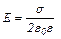
9. Зв'язок між вектором елект­ричного зміщення і напру­же­ністю електричного поля 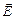для однорідного ізотропного діелект­рика:

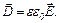
Приклад розв'язання задачі

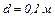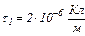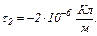Два довгі тонкі проводи розміщені пара­лельно на відстані один від одного і рів­номірно заряджені різноймен­ни­ми зарядами з ліній­ною густи­ною і Визначити нап­ру­женість поля в точці, що лежить у площині си­мет­рії на відстані від площи­ни, в якій розміщені проводи.

Розв'язання

Напруженість електричного поля створеного зарядженими про­водами в шуканій точці, дорівнює геометричній сумі напруже­ностей:

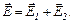
Щоб визначити напруженість поля, створеного одним із про­водів, застосуємо теорему Остро­градського-Гаусса. Тут як поверх­ню для обчислення потоку індук­ції зручно вибрати цилінд­ричну поверхню, довжина якої 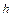і ра­діус 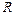. Оскільки потік через основи циліндра дорівнює нулю , а бічна поверхня пер­пен­дикулярна до лінії напруже­ності 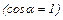, то за теоремою Остроградського-Гаусса:

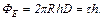
Через те, що 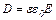, маємо

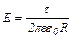
Отже,

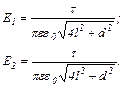
Абсолютне значення напру­женості поля 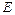дорівнює алгеб­ра­їчній сумі проекцій векторів 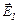і на напрям вектора :

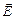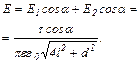
З рисунка виходить,

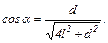
Тоді

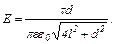
Підставимо числові значення:

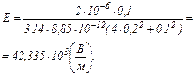
Задачі

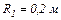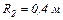20.1. На двох концентричних сферах радіусом і рівномірно розподілені заряди з поверхневими густинами 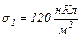і 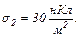Використовуючи теорему Остроградсь­кого-Гаусса, знайти напруженість поля в точці, яка віддалена від центра на відстань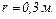

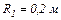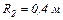20.2. На двох концентричних сферах радіусом і рівномірно розподілені заряди з поверхневими густинами 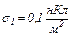і Використовуючи теорему Остроградського-Гаусса, знайти напруженість поля в точці, яка віддалена від центра на відстань .

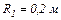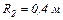20.3. На двох концентричних сферах радіусом і рівномірно розподілені заряди з поверхневими густинами 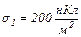і 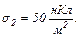Використовуючи теорему Остроградсь­кого-Гаусса, знайти напруженість поля в точці, яка віддалена від центра на відстань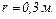

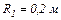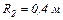20.4. На двох концентричних сферах радіусом і рівномірно розподілені заряди з поверхневими густинами 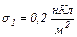і Використовуючи теорему Остроградсь­кого-Гаусса, знайти напруженість поля в точці, яка віддалена від центра на відстань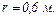

20.5. На двох нескіченних паралельних площинах рівномірно розподілені заряди з поверхневими густинами 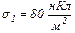і 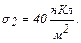Вико­рис­товуючи теорему Остроградського-Гаусса, розрахувати напруже­ність поля в точці, яка розміщена ліворуч від площин.

20.6. На двох нескінченно паралельних площинах рівномірно роз­по­ділені заряди з поверхневими густинами 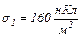і 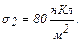Використовуючи теорему Остроградського-Гаусса, розра­хувати напруженість поля в точці між площинами.

20.7. Парафінова кулька радіусом 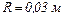рівномірно заряджена з об'ємною густиною Визначити напруженість поля на відстані 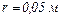від центра кульки.

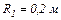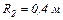20.8. На двох коаксіальних нескінченних циліндрах радіусом і рівномірно розподілені заряди з поверхневими густинами 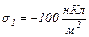і Використовуючи теорему Остроградського-Гаусса, обчислити напруженість поля в точці, яка віддалена від осі циліндра на відстань .

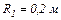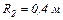20.9. На двох коаксіальних нескінченних циліндрах радіусом і рівномірно розподілені заряди з поверхневими густинами 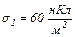і 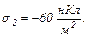Використовуючи теорему Остроградського-Гаусса, розрахувати напруженість поля в точці, яка віддалена від осі циліндра на відстань .

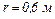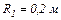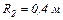20.10. На двох коаксіальних нескінченних циліндрах радіусом і рівномірно розподілені заряди з поверхневими густинами 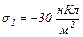і Використовуючи теорему Остроградського-Гаусса, розрахувати напруженість поля в точці, яка віддалена від осі циліндра на відстань .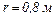

Не нашли, что искали? Воспользуйтесь поиском: