Определение исходного базиса

Чтобы приступить к решению задачи линейного программирования симплексным методом, необходимо выбрать исходный базис. Выбор ис­ходного базиса зависит от системы ограничений. Система ограничений задачи линейного программирования может быть записана в трех ос­новных формах.

1. Система записана неравенством вида ≤ (меньше или равно).

2. Ограничения задачи линейного программирования выражены ли­нейными уравнениями

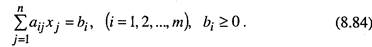
3. Ограничения задачи выражены неравенством вида ≥ (больше или равно). При ограничениях, записанных по первой форме, в уравнения вводятся свободные переменные (по одной свободной переменной в каж­дом соотношении), которые и включаются в исходный базис.

Если ограничения записаны в виде равенств (вторая форма ограни­чений), то возможны следующие приемы.

1. Если некоторая переменная входит только в j-e уравнение (соот­ношение), причем с коэффициентом, равным единице, то ее можно вклю­чить в исходный базис.

2. Ограничения, выраженные в виде равенств, записываются в следующем виде:

где: у_i - искусственная переменная, ввод которой делается с целью построения исходного базиса.

Чтобы окончательное решение имело смысл, каждая искусственная переменная у,- на заключительной симплекс-итерации должна обращать­ся в нуль. Если на последней симплекс-итерации по крайней мере одна из переменных у_i войдет в базис с положительным значением, то это означает несовместимость условий задачи, т. е. задача не имеет допусти­мых решений.

3. Если ограничения задачи выражены неравенством ≥, то в левую часть неравенств вводятся неотрицательные переменные с коэффициен­том (-1). В полученных уравнениях дополнительные переменные не могут быть приняты за базисные, так как они входят в уравнения с от­рицательным коэффициентом. Для нахождения допустимого исходного базиса, в этом случае может быть задан конкретный набор переменных, предназначенный для формирования исходного базиса.

При некоторых итерациях вычислительные процедуры, предписан­ные правилами 1 и 2, в части, касающейся перехода от одного базиса к другому, могут оказаться неоднозначно определенными. Например, когда в результате оценки коэффициентов в строке 0 две или более двух пере­менных являются по правилу 1 в равной степени «перспективными» с точки зрения улучшения пробного решения, выбор одной из этих пере­менных осуществляется произвольным способом.

Если, согласно правилу 2, две или более двух переменных промежу­точного базиса должны одновременно принять нулевые значения в силу включения в очередной базис новой переменной, из старого базиса под­лежит исключению только одна из них. Другие переменные из упомяну­тых переменных остаются в базисе, принимая при этом нулевые значе­ния. Базис, полученный в результате такой замены, называется вырож­денным.

Если на этапе применения правила 1 при выполнении какой-либо итерации обнаруживается, что ни в одну из строк ограничений перемен­ная, включенная в очередной базис, не входит с положительным коэффи­циентом, то оптимальное решение является неограниченным. В этом случае значение новой базисной переменной можно (без нарушения ус­ловия неотрицательности остальных переменных) выбирать сколь угодно большим, что приводит к неограниченному возрастанию значения целе­вой функции.

Не нашли, что искали? Воспользуйтесь поиском: