МАРШРУТИЗАЦИЯ ПЕРЕВОЗОК

Маршрутизация перевозок - это составление маршрутов движения подвижного состава или его порядок следования между пунк­тами производства и потребления. Маршрутизацию перевозок выполня­ют для однородных грузов, требующих для перевозки однотипный под­вижной состав. При маршрутизации перевозок учитывается множество ограничений, вызываемых конкретными условиями работы транспорта: объемы перевозок поставщиков и потребителей, характер грузов, время их доставки, структура парка подвижного состава и его наличие, режим работы автотранспортных предприятий и погрузочно-разгрузочных пунктов, режим работы водителей, пропускная возможность погрузочно-разгрузочных пунктов и дорожной сети, значение целевой функции и др.

Методы маршрутизации перевозок делятся на маршрутизацию перевозок помашинных отправок и маршрутизацию перевозок мелких партий грузов.

В зависимости от использования математиче­ского аппарата они делятся на методы, основанные на моделях ма­тематического программирования, и на методы, основанные на алго­ритмах задач теории расписаний.

Методы первого класса делятся на две группы. К пер­вой группе относятся задачи, в которых при известных ездках с грузом определяются потоки движения автомобильного подвижного состава без груза.

Недостатки этого метода: не обеспечивается учет всех ограниче­ний и параметров, существующих в реальной системе (время в наряде, закрепление автомобилей за клиентурой и т. д.);

возникает необходимость корректирования плана вручную (состав­ление графиков движения, графика работы погрузочно-разгрузочного пункта), что иногда приводит к отклонениям от полученного варианта.

Методы второй группы рассматривают маршруты движения как технологические способы использования ресурсов с определенными «ценами», и задаются столбцы матрицы условий. Переменными явля­ются интенсивности грузопотоков по маршрутам.

Преимущества (по сравнению с первым методом): возможность учета многих ограничений, выдвигаемых практикой; исключение ручных операций при составлении оперативного плана.

Недостатки:

большая размерность задач, определяющая трудность решения;

не учитывается наличие очередей в пунктах выполнения погрузочно- разгрузочных работ (ПРР);

алгоритмы имеют недостаточное быстродействие для оперативного управления перевозочным процессом в реальном режиме времени.

Методы второго класса построены на использовании ап­парата теории расписаний. Этапы транспортного процесса (погрузка, транспортирование, разгрузка, подача подвижного состава) представляются в виде «работ». Подвижной состав и посты ПРР выступают как «прибо­ры», предназначенные для выполнения «работ». В результате решения задачи определяется расписание выполнения «работ» (распределение ре­сурсов между работами и очередность выполнения работ).

Недостаток:

отсутствуют алгоритмы точного решения задач теории расписаний из-за большой размерности.

В настоящее время известны следующие приближенные методы ре­шения задач теории расписаний:

методы случайного поиска;

методы ситуационного управления;

методы, основанные на эвристических процедурах сокращения раз­мерности задачи.

Методы случайного поиска построены на использовании процедуры Монте-Карло. Из полученного множества решений выбирает­ся наилучшее, согласно заданному критерию оптимальности. Получен­ные этим методом решения обычно находятся на уровне решений, при­нимаемых опытным диспетчером. По этой причине они не нашли широ­кого применения.

Модели методов теории ситуационного управле­ния определенным образом формализуют реальные системы, которые работают в диалоговом режиме с ЭВМ и могут «обучаться» на опыте экспертов (диспетчеров). Так как модель перенимает опыт человека, то после «обучения» решает задачи на уровне принимавших участие экс­пертов. Требуется большое время на «обучение» ЭВМ; равно как и имеет место сложность алгоритмической и программной реализации.

Методы, основанные на эвристических процеду­рах сокращения размерности задачи, заключаются в следующем. Про­цесс составления маршрутов движения делится на несколько шагов. На каждом шаге выбирается «работа» для загрузки незанятого «прибора». Выбор осуществляется из некоторого количества «работ», которые могут быть выполнены рассматриваемым «прибором». Наличие свободы выбо­ра «работ» обуславливает существование определенного множества планов, которые отличаются друг от друга величиной некоторых показа­телей (простои «приборов», общая продолжительность выполнения за­данных «работ» и т. д.). Функции предпочтения представляют собой формальную оценку принимаемого решения на конкретном шаге фор­мирования оперативного плана.

Использование функций предпочтения позволяет сформировать план, близкий к оптимальному, не «просматривая» других возможных реше­ний. В качестве функции предпочтения могут выступать длительность выполнения очередного этапа обслуживания и др.

Для достижения оптимальности полученных планов используют комбинацию функций предпочтения как решения комбинаторных задач как в виде последовательности функций предпочтения, так и в виде обобщенного показателя.

Наибольшее применение для формирования маршрутов перевозок находит метод «совмещенной матрицы», когда при известных ездках с грузом определяется движение подвижного состава без груза. Этот метод предполагает, что план поставок выполняется совокупностью любых маятниковых и кольцевых маршрутов независимо от их протя­женности, числа звеньев и без учета подачи и возврата автомобилей. Необходимое условие - число автомобилей, прибывающих в пункт по­грузки, должно равняться числу автомобилей, выходящих из этого пункта.

Задача формулируется следующим образом: минимизировать хо­лостые пробеги

где: y_ij - число ездок без груза из j пункта выгрузки в i пункт погрузки. Рассмотрим применение этого метода на примере.

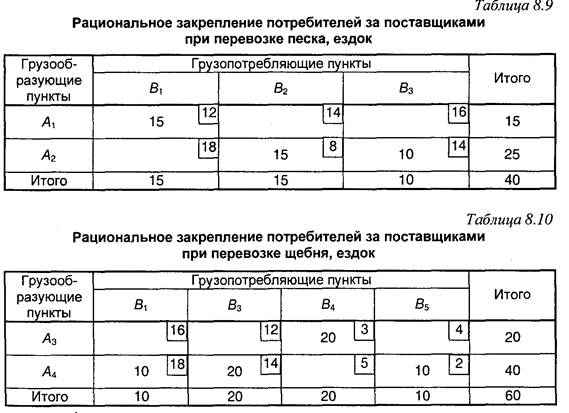
Задача 8.6. Строительные организации В₁, B₂, В₃, В₄, В₅, В₆ по­лучают строительные материалы с пяти карьеров (рис. 8.8).

Рациональное закрепление потребителей грузов за поставщиками приведено в табл. 8.9-8.11. Кратчайшее расстояние между пунктами ука­зано в табл. 8.12. Все перечисленные строительные материалы можно перевозить на одном и том же типе подвижного состава.

Необходимо так организовать перевозочный процесс, чтобы коэффициент использо­вания пробега подвижного состава имел максимально возможную вели­чину.

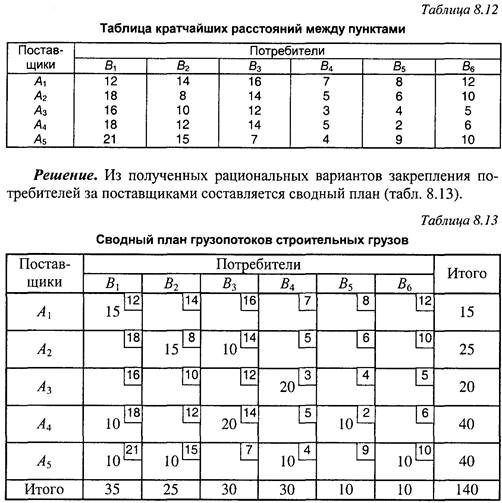
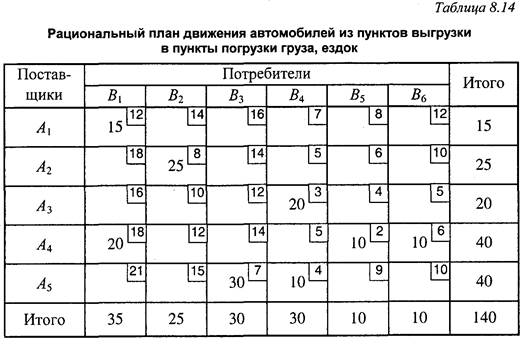
Одним из математических методов определяется рациональный план движения автомобилей из пунктов выгрузки грузов в пункты погрузки(табл. 8.14).

Для составления маршрутов можно пользоваться методом «совме­щенной матрицы». Сущность этого метода состоит в том, что в одну матрицу записываются данные о ездках с грузом и холостых ездках (табл. 8.15).

Чтобы отличать груженые ездки от холостых, желательно одни из них выделить (подчеркнуть, обвести кружком, записать другим цветом и т. д.)- В нашем примере ездки с грузом подчеркнуты. Если в клетке будут две записи, то это указывает на наличие маятникового маршрута, величи­на грузопотока которого определяется меньшей цифрой.

После того как будут выявлены маятниковые маршруты, в клетках таблицы останется только по одной цифре (табл. 8.16).

Для каждой клетки табл. 8.16, загруженной ездкой с грузом, строится контур (маршрут движения), вершины которого попеременно находятся в клетках, загруженных гружеными и холостыми ездками.

Величина грузопотока каждого маршрута определяется наименьшей величиной груженых ездок. Определение кольцевых маршрутов продол­жается до тех пор, пока не останется ни одной загруженной клетки.

В табл. 8.17 приведены рациональные маршруты движения под­вижного состава, определенные из условий нашей задачи.

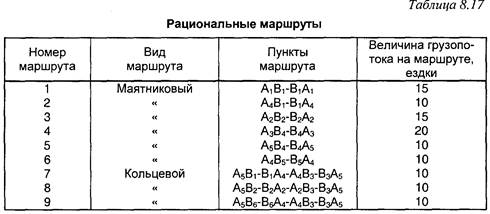
Для составления схем маршрута движения подвижного состава необхо­димо определить начальный и конечный пункт каждого маршрута.

Рациональный выбор начального и конечного пунктов маршрута позволяет сократить пробег подвижного соста­ва без груза за счет того, что в последнем обороте подвижного состава по маршруту из суммы общего пробега выпадает участок от последнего пункта выгрузки до первого пункта погрузки. В маятниковых маршрутах может быть только один вариант начального и конечного пунктов мар­шрута. При выполнении кольцевых маршрутов начало маршрута может быть из любого пункта погрузки, т. е. число вариантов равняется числу погрузочных пунктов в маршруте.

За критерий оптимальности при выборе началь­ного пункта маршрута принимается минимум суммы нулевого пробега с непроизводительным (холостым) пробегом подвижного соста­ва, т. е.минимизировать

где: 1"_х - пробег подвижного состава без груза от последнего пункта выгрузки до первого пункта погрузки, км;

l_oi - нулевой пробег при i начальном пункте маршрута, км.

Σl_xi - сумма холостых пробегов на участках маршрута, км

Не нашли, что искали? Воспользуйтесь поиском: