
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ГРАФОАНАЛИТИЧЕСКИЙ МЕТОД
Чтобы понять основные свойства линейных моделей и из чего складывается процесс получения решения задач линейного программирования, рассмотрим геометрическую интерпретацию линейного программирования, получившего название графоаналитического метода. Необходимо учитывать, что графоаналитический метод может быть использован только в том случае, если задача содержит два, максимум три неизвестных. В последнем случае приходится пользоваться пространственной моделью. Несмотря на простоту решения задач этим методом, его применение при разработке технологических процессов весьма ограничено.
Сущность графоаналитического метода рассмотрим на решении следующей задачи:
максимизировать функцию 10Х1+13Х2 (8.11)
при наличии ограничений

Решение задачи может быть найдено графически, как показано на рис. 8.2. Ограничения (8.12) и (8.13) на рис. 8.2 изображены прямыми линиями как уравнения, полученные заменой неравенств на равенства. Площадь под каждой из двух прямых эквивалентна математической формулировке, имеющей направленный смысл «меньше, чем» (<). Так как X1 и X2 не могут принимать отрицательных значений, область допустимых значений переменных ограничивается осями координат. Таким образом, многоугольник ОABC содержит в себе область значений Хх и Х2, удовлетворяющих всем имеющимся ограничениям. Множество точек, принадлежащих области, ограниченной линиями ОАВС (вместе с граничными точками), называется множеством решений. Это множество является выпуклым, т. е. любой отрезок, соединяющий две произвольным образом выбранные точки данного множества, лежит внутри или проходит вдоль границы ОABC.
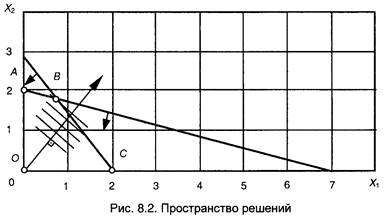
| Вершины О, А, В, С носят название экстремальных точек. Они не могут принадлежать внутренней части ни одного из отрезков, соединяющих две различные точки рассматриваемого множества. Параллельные прямые на рис. 8.2 являются графическим изображением различных значений целевой функции, которую можно записать как |

Изменяя степень достижения цели Z0, получаем на рис. 8.2 семейство параллельных изолированных прямых, уравнение которых

Из уравнения (8.16) следует, что чем выше степень достижения цели, тем выше располагается соответствующая изоцелевая прямая. Оптимальное решение определяется экстремальной точкой В, для которой

Если в формуле для целевой функции (8.11) изменить коэффициенты при переменных (при этом угол наклона параллельных линий по отношению к оси абсцисс также будет другим), то в результате точка, задающая оптимальное решение, может перемещаться. Если при наличии ограничений (8.12), (8.13), (8.14) целевая функция будет иметь вид

то в этом случае все точки, лежащие на отрезке АВ, будут являться оптимальными (рис. 8.3). Решение X1 = 0,95, Х2=1,8 будет оптимальным. Однако оптимальным будет и решение X1 = 0, Х2 = 2. Оптимальное значение целевой функции будет равно 28,0.
Проведенный анализ показывает, что решение задачи дается координатами вершин выпуклой области допустимых решений. Если решение задается координатами двух вершин, то оно дается координатами всего отрезка, соединяющего эти вершины.

| Изменение целевой оптимизирующей функции в определенных пределах не приводит к изменению решения задачи. В случае, когда в задаче имеются три переменные величины и три уравнения ограничений, например, максимизировать |

при наличии ограничений:

то приходится пользоваться пространственной моделью.
Когда ограничения являются уравнениями, то каждое из них можно считать уравнением плоскости, лежащей в трехмерном пространстве, и точка, общая этим трем плоскостям, есть единственная точка, представляющая собой допустимое решение (рис. 8.4, а). Если ограничения являются неравенствами, то область оптимальных решений образуют точки некоторого выпуклого многогранника, расположенного в первом октанте. Придавая переменной Z0, формула (8.18), различные значения, получим семейство параллельных изоцелевых плоскостей (см. рис. 8.4, а), причем большим значениям Z0 будут соответствовать плоскости, расположенные дальше от начала координат. Решение задачи дается координатами одной из вершин выпуклого многогранника допустимых решений.

Если вместо трех уравнений ограничений имеется лишь два, допустим, уравнения (8.19) и (8.20), то в этом случае областью допустимых решений окажется линия пересечения плоскостей, являющихся изображениями уравнений ограничений (рис. 8.4, б). При одном уравнении ограничений областью допустимых решений будет являться треугольник, образованный линиями пересечения плоскости, изображающей это уравнение, с плоскостями координат (рис. 8.4, в).
В случае, когда необходимо получить не максимум, а минимум функции, то многоугольник будет вогнутым.
Особенности решения задач графоаналитическим методом рассмотрим на следующих примерах
Задача 8.3. От поставщика А груз перевозится автомобилями КаMA3-5320 двум потребителям B1 и В2 на расстояние 15 и 25 км соответственно. При перевозке груза потребителю B1 на одну ездку затрачивается 1,23 ч, а потребителю В2 - 1,8 ч. Продолжительность работы автомобилей на линии -8 ч. Работая на маршруте В1, водитель делает 6 ездок, затрачивая на это 7,38 ч рабочего времени. На маршруте В2 водитель делает 4 ездки и затрачивает 7,2 ч рабочего времени. Требуется организовать работу так, чтобы максимально использовать рабочее время водителей.
Математическая модель запишется в следующем виде:
максимизировать

при наличии ограничения

где: X1 - число ездок на маршруте В1;
Х2 - число ездок на маршруте В2.

| Решение может быть найдено графически, как показано на рис. 8.5. При X1 = 0, Х2 = 4,4. При Х2 = 0, X1 = 6,5. Соединив полученные точки А и В, получим область допустимых решений X, и Х2. Левые части уравнений целевой функции (8.22) и ограничения (8.23) совпадают. Это значит, что все точки, лежащие на линии 1,23Х1+1,8Х2=8. |
будут оптимальными. Точки Q, С2 и так далее, заключенные между прямой АВ и осями координат, имеющие координатами целые числа, изображают все возможные варианты работы автомобиля. Точки, которые ближе расположены к прямой или лежат на ней, дают наилучшие - оптимальные решения.
В рассматриваемом примере точки C1 с координатами X1=5 и Х2 = 1 и С4 с координатами X1 = 2, Х2 =3 ближе всех расположены к линии АВ. В первом случае продолжительность работы водителя на линии составит
1,23-5 + 1,8*1 = 7,95 ч,
а во втором
1,23-2 + 1,8*3 = 7,86 ч.
Задача 8.4. Определить потребное число поддонов для перевозки грузов пакетами, упакованными в потребительскую тару двух размеров - А и В. Количество грузов в таре типа А составляет 600 единиц и типа В - 300 единиц. Количество тары, загружаемой на поддон различными способами, приведено в табл. 8.1.
Таблица 8.1
| Тип тары | Способы размещения тары на поддоне | |||
| А | ||||
| В |
Математическая модель задачи будет сформулирована следующим образом:
минимизировать Х{ + Х2 + Х3 + Х4 = Z0, (8.24)
при наличии ограничений

где: Xi - число поддонов, загруженных по i-способу размещения тары.
Для решения задачи начертим прямоугольную систему координат АОВ (рис. 8.6) и каждому возможному способу размещения тары на поддоне поставим точку, координаты которой соответствуют числу соответствующей тары, размещаемой на поддоне. Буквой С с индексом обозначим номер способа размещения тары на поддоне. Множество всевозможных планов размещения тары на поддоне изображается совокупностью точек выпуклого многоугольника С1 С2 С4 С3. Например, точки на отрезке С1 С2 будут указывать
| своими координатами количество тары типа А и типа В, приходящейся на один поддон в различных способах размещения их, сочетающих собой размещения по способу С1 и С2 (рис. 8.6). Из всех решений нас интересует выполнение условия комплектности, т. е. отношение числа тары А к числу тары В. В соответствии с заданием это соотношение равно 2 (600:300). Если из начала системы координат провести луч, координаты которого А= 2, В = 1, то оптимальным будет план размещения тары на поддоне, которому соответствует точка, одновременно принадлежащая многоугольнику и лучу, и имеющая наибольшие координаты, т. е. соответствующая плану наибольшего использования площади поддонов. Такой точкой будет Р, лежащая на отрезке С1 С3. Это указывает на то, что оптимальный план размещения тары на поддонах представляет собой комбинацию размещения тары по способу C1 и С3. |  |
Обозначим через δ долю поддонов, загружаемых по способу C1, а остальную часть (l-δ) - по способу С3, долю одного и другого способа размещения поддонов найдем из условия комплектности

Минимальное число поддонов Z0 определится из уравнения
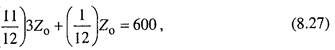
откуда Z0 =212. Таким образом, по способу C1 будет загружено 194 поддона и по способу С3 - 18.
МЕТОД ПОТЕНЦИАЛОВ
Метод потенциалов линейного программирования применяется при решении задач, связанных с распределением на транспортной сети грузопотоков: закрепление потребителей грузов за поставщиками, распределение парка подвижного состава по автотранспортным предприятиям, закрепление маршрутов работы подвижного состава за автотранспортными предприятиями и другие задачи. Задача закрепления потребителей за поставщиками получила название классической транспортной задачи. Решение такой задачи сводится к выбору транспортных маршрутов, по которым продукция различных предприятий перевозится на несколько конечных пунктов назначения.
Математическая модель классической транспортной задачи в общем виде записывается в следующей форме:
минимизировать

при ограничениях
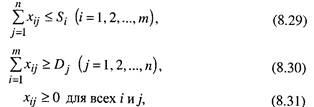
где: m - число поставщиков;
n - число потребителей;
Xij - объем перевозок между i и j пунктами;
Si- - ограничения по предложению;
Di - ограничения по спросу;
aij - расстояние от пункта i до пункта j.
Условия задачи можно представить следующим образом. Каждый поставщик должен дать потребителям столько продукции, сколько у него есть, т. е.

Каждый потребитель должен получить столько, сколько ему требуется, т. е.

Необходимо найти такой вариант плана перевозок, чтобы транспортная работа была минимальна, т.е.

Запись и решение транспортной задачи методом потенциалов выполняется в таблично-матричной форме. Совокупность всех элементов матрицы хij называется планом перевозок или распределением поставок. Элементы матрицы называются показателями критерия оптимальности.
В каждой конкретной транспортной задаче можно найти бесчисленное множество вариантов плана перевозок. План перевозок считается допустимым, если все возможности поставщиков используются, а спрос всех потребителей удовлетворяется. Такая модель транспортной задачи называется закрытой в силу сбалансированности спроса и предложения. Транспортная задача, в которой спрос не равен предложению, называется открытой моделью.
Если допустимый план удовлетворяет условию (8.34), то он является оптимальным. В условии (8.34) сформулирована цель задачи или ее целевая функция. При решении транспортной задачи в качестве целевой функции могут приниматься следующие показатели: минимум тонно-километрового пробега, минимум провозных плат, минимум эксплуатационных расходов, минимум тонно-часов транспортирования и др.
Критерий «минимум тонно-километрового пробега» (показатель критерия - расстояние) наиболее прост для применения и определения. К его недостаткам следует отнести то, что при одинаковом расстоянии транспортирования могут быть различные затраты (движение подвижного состава по различным дорожным покрытиям, перевозки по дорогам с различной интенсивностью движения и т. д.).
Критерий «минимум провозных плат» (показатель критерия - тарифы) применяется для получения схемы грузопотоков, обеспечивающей минимальные затраты грузоотправителей. К недостаткам этого критерия следует отнести то, что тарифы не обладают свойством аддитивности, т. е. суммы тарифных плат от пункта А до пункта Б и от пункта Б до пункта В не идентичны тарифу от пункта А до пункта В. Это не дает возможности использовать тарифы в качестве критерия оптимальности при сетевой постановке задачи, а также при использовании машинных методов составления матриц.
Критерий «минимум эксплуатационных расходов на транспортирование грузов» (показатель критерия - себестоимость транспортирования) отражает затраты автотранспортного предприятия, осуществляющего выполнение перевозок. Этот критерий может также использоваться при распределении перевозок между различными видами транспорта. Его недостатками являются: себестоимость транспортирования рассчитывается на обезличенный груз и не учитывает затрат, возникающих при перевозке отдельных видов специальных грузов; не учитывает изменение затрат на погрузочно-разгрузочные работы при использовании различных видов подвижного состава; сложность расчета себестоимости транспортирования по отдельным участкам дорожной сети.
Критерий «минимум тонно-часов транспортирования груза» (показатель критерия - время транспортирования) может применяться при перевозке скоропортящихся грузов, овощей, живности и другой продукции. К его недостаткам относится то, что он не учитывает затрат, связанных с транспортированием груза.
Линейные уравнения, описывающие условия транспортной задачи, отражают пропорциональные зависимости. Наличие линейных зависимостей - обязательное условие применения методов линейного программирования. Однако для транспортной задачи это требование условно. Например, затраты на транспортирование грузов не прямопропорциональны расстояниям транспортирования, однако они используются в качестве показателей целевой функции.
Чтобы задача имела допустимое решение, требуется, чтобы общие ресурсы поставщиков были не меньше общего спроса потребителей Si ≥ Dj, а также естественным представляется и требование неотрицательности объема поставок и спроса, т. е. Si ≥ 0, Dj≥ 0.
Рассмотрим применение метода потенциалов на следующем примере:
Задача 8.5. Из трех грузообразующих пунктов A1, А2, А3 необходимо перевезти однородный груз четырем потребителям Bl, В2, B3, B4. Количество груза в пункте А1 = 300 т, в пункте А2 = 500 т, A3 = 800 т. Спрос потребителей на данный груз составляет: В1 = 200 т, В2 = 350 т, B3 = 650 т, В4 = 400 т. Расстояния между грузоотправителями и грузополучателями приведены в табл. 8.2. Необходимо так закрепить потребителей груза за грузополучателями, чтобы общая транспортная работа была минимальной (показатель критерия оптимальности - расстояние).
Таблица 8.2
Расстояние между грузообразующими и грузопоглощающими пунктами
| Грузообразующие пункты | Грузопоглащающие пункты | |||
| В1 | В2 | В3 | В4 | |
| Расстояния, км | ||||
| А1 | ||||
| А2 | ||||
| А3 |
Для решения задачи обозначим через хij количество тонн груза, которое должно быть перевезено от i-поставщика j-потребителю. Тогда математическая модель задачи выразится системой уравнений (8.35), а целевая функция, представляющая собой сумму произведений расстояний на соответствующий объем перевозок груза в тоннах, уравнением (8.36).
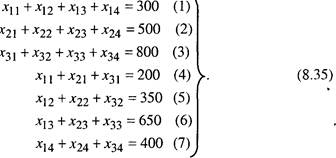
Минимизировать
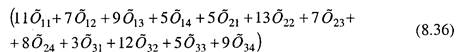
Полученная система уравнений (8.35) является линейно зависимой, так как любое ее уравнение можно представить в виде линейной комбинации остальных уравнений. Действительно, если из суммы уравнений 1, 2, 3 вычесть сумму уравнений 4, 5, 6, то получим уравнение 7 и т. д. Число линейно независимых уравнений должно быть меньше на одно общего числа уравнений в системе, т. е. базис системы должен быть равен количеству уравнений в системе ограничений за вычетом единицы. Так как общее число уравнений в системе определяется суммой поставщиков и потребителей, то в базисе должно быть уравнений
т + п-1, (8.37)
где: m - число поставщиков;
n - число потребителей.
Для решения транспортной задачи методом потенциалов составляется базисный план, который заносится в таблицу, называемую матрицей распределительного метода.
Матрица - прямоугольная таблица чисел, состоящая из m строк и n столбцов, в которой на пересечении строк и столбцов, обычно в правых верхних углах, указывается расстояние между данным поставщиком и потребителем (в общем случае указывается показатель целевой функции).
К базисному плану предъявляются следующие требования:
он должен быть допустимым, содержать m + n — 1 загруженных клеток, чтобы загруженные клетки были расположены в порядке вычеркиваемой комбинации. Для сокращения числа итераций при последующем решении желательно, чтобы базисный план был, возможно, ближе к оптимальному.
Напомним, что план считается допустимым, если все возможности поставщиков используются, а спрос всех потребителей удовлетворяется. Однако для решения транспортной задачи методом потенциалов (или любым другим методом линейного программирования) необходимо, чтобы матрица имела определенное число загруженных клеток и чтобы загруженные клетки были расположены в порядке вычеркиваемой комбинации.
Число неизвестных Х в задаче равно произведению числа строк m на число столбцов n. Максимальное число уравнений, которое можно получить при решении транспортной задачи, определяется суммой поставщиков и потребителей, т. е. т + п. В этом случае, как показано выше, система уравнений является линейно зависимой. Для решения транспортной задачи базис системы должен содержать т + п-1 уравнений, а следовательно, в матрице должно быть т + п-1 загруженных клеток.
Условие вычеркиваемой комбинации загруженных клеток означает, что если, последовательно проходя по строкам и столбцам матрицы, можно вычеркнуть все загружаемые клетки, то их комбинация считается вычеркиваемой. При этом загруженная клетка вычеркивается, если она единственная в своей строке или своем столбце.
Самый простой способ составления базисного плана - это так называемый способ северо-западного угла. Сущность этого способа заключается в следующем. Распределение груза по потребителям начинается с клетки А1 В1 (табл. 8.3). Если предложение больше спроса, то следующая цифра ставится в клетке А1 В2 и т. п.
Таблица 8.3
Базисный план, составленный способом северо-западного угла
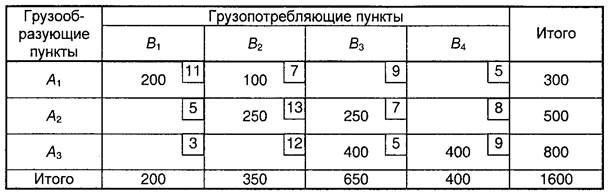
Клетки таблицы, в которых отмечено количество груза, перевозимого от грузоотправителя к данному грузополучателю, называются загруженными. Остальные клетки - незагруженными. Способ северо-западного угла является плохим способом составления базисного плана, так как в большинстве случаев дает базисный план, очень далекий от оптимального. Положительная сторона его заключается в том, что он очень прост и обеспечивает получение т + п-1 загруженных клеток.
При полученном базисном плане закрепления поставщиков за потребителями (табл. 8.3), транспортная работа составит
200 • 11 +100 • 7 + 250 • 13 + 250 • 7 + 400 • 5 + 400 -9 = 13500 т-км.
Несколько лучшими способами составления базисного плана являются способы наименьшего элемента по столбцу или наименьшего элемента по строке. При составлении базисного плана способом наименьшего элемента по столбцу поочередно в столбцах матрицы отмечаются клетки с минимальным значением ау и в
них заносятся поставки. Если при записи поставок спрос по столбцу удовлетворен не полностью, ищется следующий по величине показатель aij, и так до полного удовлетворения спроса. Только после этого переходят на следующий столбец. Когда в столбце два или несколько одинаковых по величине минимальных показателей aij, то поставки могут быть размещены в любом из них. Результаты составления базисного плана этим способом приведены в табл. 8.4.
Таблица 8.4
Базисный план, составленный способом наименьшего элемента по столбцу

При базисном плане, полученном способом наименьшего элемента по столбцу (табл. 8.4), транспортная работа составит
200-3 + 300-7 + 50-12 +100-7 +550-5 + 400-8 = 9950т-км.
Базисный план получился лучше (транспортная работа сократилась на 3550 т-км), однако нельзя сказать, является ли он оптимальным или нет. Для ответа на этот вопрос необходимо составленный базисный план проверить на оптимальность. Для этих целей разработано несколько методов. Наиболее широкое применение находят методы потенциалов (метода МОДИ), Хичкока, Креко.
Идея метода потенциалов была высказана Л. В. Канторовичем в 1940 г. В 1951 г. американский ученый Дж. Д. Данциг предложил ту же идею, назвав ее модифицированным распределительным методом (МОДИ). Идея метода потенциалов, или метода МОДИ, заключается в том, что для проверки допустимого базисного плана на оптимальность определяются особым образом числа, называемые потенциалами. Главное требование к потенциалам заключается в том, чтобы каждый показатель aij в загруженной клетке был равен сумме потенциалов своих строки и столбца
aij=Vi+Vj, (8.38)
где: Ui - значение потенциала строки;
Vj - значение потенциала столбца.
Совершенно безразлично, с какой строки или столбца начинать определение потенциалов. Безразлично также, каким по величине взять первый по счету потенциал, так как произвольно определяется только первый потенциал. Все остальные потенциалы жестко связаны с ним, и после того, как первый потенциал установлен, он определяется единственно возможным способом. Определенные потенциалы строк и столбцов должны обеспечить значение потенциалов загруженных клеток равными нулю.
Потенциалы незагруженных (свободных) клеток определяются по формуле

где: Еij - потенциал свободной клетки.
При решении задач на минимум оптимальный вариант допустимого плана получается в том случае, когда во всех загруженных клетках стоят нулевые потенциалы, а потенциалы всех свободных клеток являются положительными величинами. Наличие свободных клеток с отрицательными значениями потенциалов показывает, что имеются резервы улучшения варианта решения.
При решении задач на максимум оптимальный вариант допустимого плана получается тогда, когда во всех загруженных клетках стоят нулевые потенциалы, а потенциалы всех свободных клеток являются отрицательными величинами.
Проверим на оптимальность базисный план, составленный способом наименьшего элемента по столбцу. Для этого матрицу распределительного метода дополним одним столбцом и строкой (табл. 8.5). Поставим в строке A1 величину потенциала, равную нулю. Тогда, согласно формуле (8.38), потенциал столбца В2 будет равен 7. Потенциал строки A3 будет равен 5, а столбца B3 - 0 и т. д. Потенциалы незагруженных клеток находим по формуле (8.39).
В результате проверки допустимого плана на оптимальность получена клетка А2В2, имеющая отрицательный потенциал. Это указывает на то, что план не оптимален и необходимо выполнить перераспределение закрепления поставщиков за потребителями. Это выполняется следующим образом. Строится контур. Контуром называется замкнутая ломаная линия, образованная прямыми отрезками, углы соединений между которыми равны 90°. Строится контур так, чтобы все углы, кроме одного, располагались в загруженных клетках, а один угол в свободной, наиболее потенциальной клетке. При соблюдении этих правил для каждой свободной (незагруженной) клетки можно построить только один контур. Определяют положительные (+) и отрицательные (-)углы контура. Первый положительный угол лежит в незагруженной клетке, для которой строится контур, рядом с ним находятся отрицательные углы и т. д.
Таблица 8.5
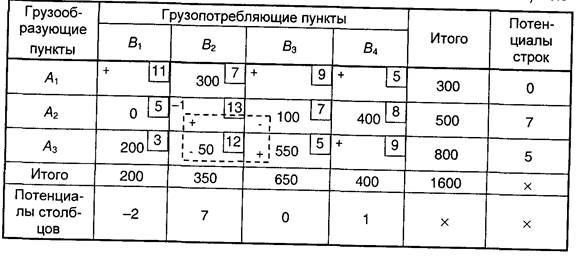
Определяется наименее загруженная клетка, занятая отрицательным углом контура. Количество груза, указанное в этой клетке, отнимается из всех клеток, занятых отрицательными углами контура, и прибавляется во все клетки контура с положительными углами.
Ранее загруженные клетки, которые не оказались расположенными в углах контура, переносятся в матрицу нового варианта закрепления потребителей груза за поставщиками без изменения (табл. 8.6).
Таблица 8.6
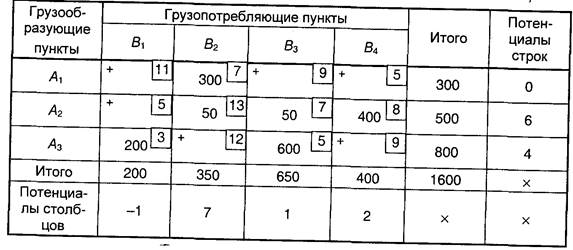 Проверка этого варианта допустимого плана показывает, что получен оптимальный вариант, так как все незагруженные клетки имеют положительные потенциалы, а потенциалы загруженных клеток равны нулю. Объем транспортной работы при оптимальном закреплении поставщиков за потребителями составляет
Проверка этого варианта допустимого плана показывает, что получен оптимальный вариант, так как все незагруженные клетки имеют положительные потенциалы, а потенциалы загруженных клеток равны нулю. Объем транспортной работы при оптимальном закреплении поставщиков за потребителями составляет
200-3 + 300-7 + 50-13 + 50-7 + 600-5 + 400-8 = 9900 т-км.
Последовательность решения транспортной задачи методом потенциалов схематически показана на рис. 8.7.
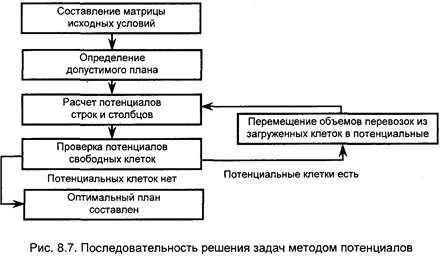
| Другие способы составления базисного плана. При решении транспортных задач методом потенциалов число итераций можно значительно сократить за счет более удачного составления первоначального - базисного плана поставок. |
Ранее отмечалось, что способ северо-западного угла является самым неудачным способом составления базисного плана. Распределение поставок способом наименьшего элемента по столбцу или по строке значительно улучшает базисный план поставок. Помимо этих приемов, улучшающих базисный план, рассмотрим еще три способа: способ аппроксимации У. Фогеля, способ последующего анализа (способ стрелок) и способ двойного предпочтения.
Способ аппроксимации У. Фогеля. По мнению У. Фогеля, его способ может заменить во многих случаях методы линейного программирования. На самом деле его можно применять только для составления базисного плана, а затем для решения задачи использовать обычную процедуру линейного программирования.
При составлении базисного плана поставок способом аппроксимации У. Фогеля исходные данные заносятся в таблицу, которая отличается от матрицы метода потенциалов тем, что имеет дополнительную строку и столбец разностей (табл. 8.7).
Таблица 8.7

Процесс составления базисного плана начинается с определения разностей между двумя наименьшими элементами каждой строки и каждого столбца матрицы.
Так, в столбце минимальный элемент равен 3 в клетке А3В1. Следующий за ним по величине элемент, равный 5, находится в клетке А2В1. Разность между ними равна 2. Эта и другие разности по строкам и столбцам записаны в табл. 8.7.
Затем из всех разностей столбцов и строк выбирается наибольшая. В нашем примере это цифра 5 в столбце В2. Клетка с наименьшим расстоянием (при решении задачи на минимум), расположенная в строке или столбце, имеющая наибольшую разницу, загружается максимально возможным количеством груза (с учетом потребности грузопотребляющего и возможности грузообразующего пунктов).
Смысл способа У. Фогеля заключается в следующем. Найденные разности показывают, насколько больше будут расстояния, если в соответствующем столбце или строке поставка будет записана не в клетку, где находится минимальный в этом столбце или строке элемент, а в клетку, где находится элемент, следующий за ним по величине. Там, где разность оказывается наивысшей, будут наибольшие потери на единицу продукции, если поставка не попадет в клетку с наименьшим оптимизирующим элементом.
В нашем примере, записав максимальную поставку в клетку А1 В2 в количестве 300 т, исключаем показатели критерия оптимальности по этой строке, поскольку мощность поставщика А1 полностью исчерпана, и вновь определяем разности между наименьшими элементами по строкам и столбцам матрицы (табл. 8.8.)
Таблица 8.8

Если оказывается несколько одинаковых разностей, имеющих максимальное значение (в нашем примере столбцы В1 В3 и строки А2 и A3), то в соответствующих им столбцах или строчках находят и загружают седловую точку. Седловой точкой называют клетку таблицы, расстояние которой имеет наименьшее значение (при решении задачи на минимум) из всех расстояний ее строки и столбца или наибольшее значение при решении задачи на максимум.
При наличии независимых седловых точек, т. е. расположенных в различных строках и столбцах, загружают их одновременно. Когда седловые точки отсутствуют, находят дополнительные разницы. Загружается клетка, у строки или столбца которой дополнительная разница будет наибольшей.
В нашем примере седловой точкой будет клетка А3В1 в которую записывается максимально возможная поставка, и т. д.
Способ последующего анализа (способ стрелок). Первоначальное закрепление потребителей за поставщиками, начиная с первого столбца с учетом наименее возможного расстояния транспортирования, потребности грузопотребителя и возможности поставщика (см. табл. 8.4). Полученный базисный план анализируется с целью выявления возможностей его улучшения. В строке А3 можно передвинуть из клетки А3В2 в клетку A3В1 50 т, а из клетки А2В3 в клетку А2В2 вместо этого - 50 т. В результате этого в первом случае расстояние перевозки увеличится на 7 км, а во втором случае сократится на 6 км. Суммарное сокращение расстояния перевозки составит 1 км.
Закончив улучшение плана поставок по строкам матрицы, переходят к рассмотрению возможности улучшения базисного плана путем передвижения загрузок клеток по столбцам. Передвижение будет рациональным, если сумма расстояний, указанных в углах клеток, из которых перемещается загрузка, будет больше, чем сумма расстояний клеток, в которые передвигается поставка. Полученное распределение проверяется на оптимальность.
Способ двойного предпочтения. В первом столбце матрицы отыскивается минимальный элемент и проверяется, минимальный ли он также и в своей строке. Если да, то эта клетка отмечается звездочкой и загружается с учетом ограничений по спросу и предложению. В зависимости от соотношения спроса и предложения из последующего рассмотрения исключаются все элементы данного столбца или данной строки. После этого переходят к следующему столбцу. Если минимальный элемент столбца не является одновременно минимальным элементом строки, то сразу же переходят к рассмотрению следующего столбца. Пройдя последний столбец, переходят к первому из оставшихся и так далее, пока распределение не будет закончено. Дальнейшее решение производится по алгоритму метода потенциалов.
Если при составлении базисного плана число загруженных клеток получается больше, чем m + n-1, то при проверке на оптимальность для какой-либо строки или столбца будут найдены два потенциала. Чтобы устранить такую ситуацию, нужно произвести следующие действия:
построить для загруженной клетки, по которой определены два потенциала, контур так, чтобы все его углы лежали в загруженных клетках;
углы контура обозначить попеременно знаками «плюс» и «минус». Углу, лежащему в загруженной клетке, для которой построен контур, присваивается знак «плюс»;
выявить наименьшую загрузку в клетках, занятых углами со знаком «плюс», вычесть ее из всех клеток и прибавить во все клетки, занятые углами со знаком «минус».
В результате таких действий число загруженных клеток сократится. При этом ранее найденное решение либо улучшится, либо останется прежним.
Если число загруженных клеток при составлении базисного плана окажется меньше, чем т + п - 1, то недостающее число клеток загружают нулями. Загружать следует те клетки, которые лежат на пересечении строк и столбцов, не имеющих потенциалы, со строками или столбцами, для которых потенциалы уже определены и имеют наименьшие значения показателя критерия оптимальности.
Дополнительные условия при решении транспортных задач методом потенциалов. Предложение больше спроса. Условия задачи записываются в таблицу, в которую вводится фиктивный столбец Р с ограничением по спросу, равный разности между предложением и спросом. Так как груз никуда не вывозится, то в углах клеток столбца Р ставятся нули. Задачу решают по алгоритму метода потенциалов, рассматривая столбец Р как потребитель груза.
Если спрос превышает предложение,™ подобным образом такие задачи решать нельзя. В этом случае один из потребителей не получит груза, а неполучение груза различными грузополучателями оказывает неодинаковое влияние на конечные результаты работы этих предприятий.
Запрещение корреспонденции. Если необходимо по каким-либо причинам наложить запрет на перевозку груза из пункта A1 в пункт В1, то для этого достаточно вместо реального элемента целевой матрицы, стоящего в клетке А1 В1, поставить очень большую величину М, которая больше любого наперед заданного числа, имеющегося в данной задаче.
Обязательная поставка. Если из пункта Аi- в обязательном порядке необходимо перевезти в пункт Bj какой-то объем груза, то в этом случае величина обязательной поставки вычитается из суммы спроса и суммы предложений и при решении задачи не учитывается. При определении окончательного результата затраты, связанные с обязательным объемом перевозок, прибавляются к полученному оптимальному варианту.
Открытая модель возникает в случаях, когда отсутствует какая-либо из групп ограничений - спрос или предложение. Это означает, что любой потребитель может взять всю сумму имеющихся у поставщиков материалов или любой из поставщиков может удовлетворить спрос всех потребителей данного материала.
Решение задачи. Если отсутствуют ограничения по предложению, то ограничения по спросу в каждом столбце таблицы переносятся в клетки с оптимальным элементом целевой матрицы данного столбца, а при отсутствии ограничений по спросу - в клетку каждой строки.
Признаки наличия альтернативных решений. При решении задач методом потенциалов может быть, что при одном и том же значении целевой функции имеется несколько базисных планов с разными вариантами грузопотоков. Признаком наличия альтернативного оптимального плана при решении задач методом потенциалов является наличие равенства суммы потенциалов с элементом целевой матрицы в одной или нескольких свободных клетках.
Не нашли, что искали? Воспользуйтесь поиском: