Двойственность задач линейного программирования

В теории линейного программирования существует понятие двойст­венности, которое позволяет унифицированным образом устанавливать взаимосвязи для всех приемов и методов анализа моделей на чувстви­тельность. Рассмотрим понятие «двойственность» на двух следующих задачах:

максимизировать

при ограничениях

минимизировать

при ограничениях

Условно назовем первую задачу исходной, а вторую двойственной (по отношению к первой). Рассмотрим это на примере.

Исходная задача:

максимизировать

Z = 6X₁+5X₂+3X₃ → max, (8.101)

при ограничениях

Двойственная задача:

минимизировать

Z = 10Y₁ + 20У₂ → min, (8/103)

при ограничениях

Образно говоря, двойственная задача - это на 90 градусов поверну­тая исходная задача:

1) j-й столбец, составленный из коэффициентов, фигурирующих в ог­раничениях исходной модели, совпадает с j-й строкой, составленной из коэффициентов, фигурирующих в ограничениях двойственной модели;

2) строка, составленная из коэффициентов в выражении для целе­вой функции, совпадает со столбцом, составленным из констант, фи­гурирующих в правых частях ограничений двойственной модели;

3) столбец, составленный из констант, фигурирующих в правых час­тях ограничений исходной модели, совпадает со строкой, составленной из коэффициентов в выражении для целевой функции двойственной мо­дели;

4) направление знаков неравенства в исходной модели противопо­ложно направлению знаков неравенства в двойственной модели. Требо­вание максимизации в исходной задаче заменено требованием миними­зации в двойственной задаче.

Теорема двойственности:

а) если исходная и двойственная ей задача имеют допустимые реше­ния, то: существует оптимальное решение X_j* (j = 1,2,..., п) исходной задачи; существует оптимальное решение Y_i* (i = 1,2,..., т) двойственной задачи;

имеет место следующее соотношение:

б) если исходная (двойственная) задача допускает оптимальное ре­шение, для которого значение целевой функции ограничено, то соответ­ствующая ей двойственная (исходная) задача допускает оптимальное ре­шение при том же значении целевой функции.

Если существует допустимое решение двойственной задачи, для ко­торого значение целевой функции совпадает со значением целевой функ­ции исходной задачи, то решения обеих задач являются оптимальными.

Решение двойственной задачи

В качестве примера рассмотрим ранее решенную Задачу о распреде­лении ресурсов:

максимизировать Z = 4Х₁ +5Х₂ + 9Х₃ + 11Х₄ → mах,

Двойственная задача будет формироваться следующим образом:

минимизировать Z = 15Y₁ + 120У₂ + 100Y₃ → min, (8.108)

при ограничениях

Оптимальные значения переменных двойственной задачи:

а) коэффициенты при свободных переменных в строке 0 на последней симплекс-итерации при решении задачи максимизации совпадают с оп­тимальными значениями переменных двойственной задачи;

б) коэффициент при X j в строке 0 на последней симплекс-итерации

представляет собой разность между левой и правой частями j-го ограни­чения двойственной задачи, соответствующую оптимальному решению последней.

Рассмотрим коэффициенты при трех свободных переменных в строке 0 на заключительной симплекс-итерации (см. формулу (8.87)). Со­гласно утверждению, приведенному выше, оптимальными значениями переменных двойственной задачи являются следующие:

Убедимся, что выполняются условия (8.105)

а также то, что значение целевой функции двойственной задачи совпада­ет со значением целевой функции исходной задачи

Решение (8.106) должно быть оптимальным, поскольку удовлетворя­ются все ограничения и, кроме того, значения целевых функций исход­ной и двойственной задач совпадают. Наконец, вычислим разность меж­ду левыми и правыми частями соотношений (8.107)

т. е. получаем значения коэффициентов при Х₂ и Х₄ в строке 0 сис­темы уравнений (К), что согласуется с отверждением, сформулирован­ным выше.

Таким образом, симплексный метод можно рассматривать как способ получения пробных решений двойственной задачи путем определения допустимых решений исходной задачи. Как только удается найти допус­тимое решение этих двух задач, процесс итерации заканчивается.

Продолжение анализа на чувствительность.

Выше говорилось о том, что теорема двойственности позволит лучше разобраться в анализе линейных моделей на чувствительность.

Обращаясь к примеру, рассмотренному выше, разберем уравнение

Если коэффициент при Х₂ в выражении для целевой функции поло­жить равным 5 + δ, то в правой части соотношения (8.110) также будет стоять 5 + δ. Подставив в (8/110) оптимальные значения двойственной задачи (8.106), получим, (с учетом замены (5 + δ)):

Таким образом, решение двойственной задачи остается допустимым, если δ не превышает 3/7. Если же δ принимает значение, превышаю­щее значение 3/7, то это решение не является более допустимым и, сле­довательно, рассматриваемое решение исходной задачи не является более оптимальным.

В каких случаях в базис можно вводить новую переменную? Предпо­ложим, что в нашу задачу вводится дополнительная переменная, причем дополнения к строкам имеют следующий вид:

Пусть при переменной Х₈ в выражении для целевой функции стоит коэффициент С₈. При каком значении Cg целесообразно ввести в базис переменную Х₈? Соответствующее соотношение двойственной задачи имеет вид:

Подставив сюда полученные оптимальные значения переменных двойственной задачи, получим

Значит при С₈≥14 переменную нужно включать в базис. Оптимальное значение каждой переменной двойственной задачи определяет положительное или отрицательное приращение значения целевой функции за счет единичного приращения (положительного или отрицательного) значения константы в правой части соответствующего ограничения при условии, что рассматриваемый базис остается допустимым.

Оптимальное значение переменных двойственной задачи называют скрытыми доходами. Почему в нашей задаче увеличение объема материала типа А не приводит к увеличению прибыли? Это объясняется тем, что запас материала типа А превышает имеющиеся в нем потребности, что видно из того обстоятельства, что свободная переменная Xg входит

в оптимальный базис. Увеличение заведомо избыточного ресурса не мо­жет увеличить прибыль.

СЕТЕВОЕ ПЛАНИРОВАНИЕ В УПРАВЛЕНИИ

Сетевые модели в управлении представляют собой систему совре­менных расчетных методов планирования, организационных меро­приятий и средств контроля за выполнением плана. В сравнении с тради­ционными методами они повышают эффективность управления посред­ством рациональной организации производственных процессов и мобилизации скрытых временных и материальных ресурсов.

Практически всякую производственную ситуацию можно рассмат­ривать как модель. Модели, используемые в процессе управления, пред­ставляют либо в графической форме, либо в форме экономико-математических моделей. Сетевая модель, как правило, изображается графически. Сетевое планирование (графическая форма представления модели) появилось как результат исследования вопроса: будет ли приме­нение математических методов способствовать лучшему решению ти­пичных задач календарного планирования проектов (под проектом понимается любой комплекс работ,/необходимых для достижения единой поставленной цели). Полученные результаты (конец 50-х го­дов) показали, что выражение взаимосвязи работ проекта в виде сете­вой модели обеспечивает получение необходимого эффекта, который нельзя получить с помощью ранее применяемых методов. Например, если завершение проекта необходимо ускорить, то нужно четко опре­делить какие работы необходимо ускорить и насколько, чтобы получить выигрыш во времени при наименьших затратах.

Сетевые модели используются на автомобильном транспорте при планировании и организации сложных и трудоемких работ с большим числом исполнителей. К сетевым моделям можно отнести графики ис­пользования подвижного состава |(рис. 8.15), технологические схемы пе­ревозки грузов, а также различные сетевые графики и сетевые матрицы. При построении сетевого графика используются три основных по­нятия: работа, событие и путь.

Работа - это трудовой процесс, требующий затрат времени и ре­сурсов (например, анализ информации, оценка обстановки, выполнение этапа разгрузки, транспортирование и др. На графике работа изобра­жается в виде сплошной стрелки.

В понятие «работа» включается процесс «ожидания», т. е. процесс, не требующий затрат труда и ресурсов, но требующий затрат времени. В управлении это может быть ожидание получения информации от сторонних организаций, ожидание погрузки, разгрузки и т. д. Процесс ожидания изображается пунктирной стрелкой с обозначением над ней продолжительности ожидания. Понятие «зависимость» ме­жду двумя или несколькими событиями свидетельствует об отсутствии необходимости в затратах времени и ресурсов, но указывает наличие свя­зи между работами (начало одной или нескольких работ зависит от вы­полнения других работ). Зависимость изображается в виде пунктирной линии (стрелки) без обозначения времени. Событиями называются на­чальные и конечные точки работы.

Событие - это результат выполнения всех работ, входящих в данное событие, позволяющий начинать все выходящие из него рабо­ты. На сетевом графике событие изображается в виде кружка. Собы­тие не является процессом и поэтому не сопровождается затратами вре­мени или ресурсов.

Ни одно событие не может произойти до тех пор, пока не будут за­кончены все входящие в него работы.

Ни одна работа, выходящая из данного события, не может начать­ся до тех пор, пока не произойдет данное событие.

Ни одна последующая работа не может начаться раньше, чем бу­дут закончены все предшествующие ей работы.

Путь - это непрерывная последовательность работ, начиная от ис­ходного события и кончая завершающим. Путь, имеющий наибольшую продолжительность, называется критическим и на графике обознача­ется утолщенной или сдвоенной стрелкой. Так как критический путь имеет самую большую продолжительность по сравнению с другими пу­тями, то (эти пути) он имеет запас времени, что дает возможность для оперативного маневрирования ресурсами.

Для построения сетевого графика необходимо в технологической по­следовательности установить:

какие работы должны быть завершены до начала данной работы; какие работы должны быть начаты после завершения данной ра­боты;

какие работы необходимо выполнять одновременно с выполнением данной работы.

При построении сетевых графиков применяется несколько правил:

правило обозначения работ;

запрещения «тупиков»;

запрещения необеспеченных событий;

правило изображения «поставки»;

правило организационно-технологических связей между рабо­тами. /

Правило обозначения работ. В сетевом графике между двумя смежными событиями может проходить только одна стрелка (график I).

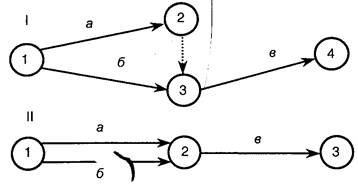
Поэтому, когда две и более работы выходят из одного и то­го же события, выполняются параллельно и заканчиваются одним и тем же событием, при расчете модели невозможно определить пара­метры этих работ (график II). На графиках обозначено 1,2,3,4- событие а, б, в- работа.

Правило запрещения «тупиков». В сетевом графике не должно быть событий («тупиков»), из которых не выходит какая- либо работа, за исключением завершающего события сети.

Например, событие 3 - тупиковое, означающее, что введены лишние работы или имеется ошибка в технологии выполнения работ.

Правило запрещения необеспеченных собы­тий.

В сетевом графике не должно быть событий, кроме начального, в которые не входит ни одной работы.Например, работа а не будет выпол­нена, так как событию 3 не предшествует ни одной работы (не заданы ис­ходные условия для начала этой работы).

Правило изображения «поставки». «Поставка» - это результат, который получен за пределами системы, т. е. не является ре­зультатом работы данного коллектива. «Поставка» изображается кружком, внутри которого поставлен крестик.

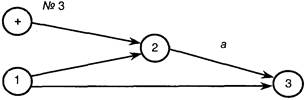
Рядом с кружком указы­вается номер спецификации, раскрывающей содержание поставки. Из рисунка видно, что «поставка» необходима для выполнения рабо­ты а. Номер 3, стоящий у кружка «поставка» - это третья строка в специ­фикации.

Правило организационно-технологических связей между работами. В сетевом графике учитываются или только непосредственные связи между работами, или связь через зависимость.

На рисунке показано несколько работ. Работе г предшест­вует только работа в (график I). Но если работе г непосредственно предшествуют работы в и а, то модель должна быть изображена по иному (график II).

Задача 8.13. Необходимо выполнить следующие работы: а, б, в, г, д. Работы а и б начинаются одновременно. Работа в должна выполняться после работы а. Работа г должна выполняться после работы б. Работа д - после выполнения работ в и г. Эту технологическую последовательность работ запишем следующим образом:

Предшествующие работы Данные работы

- а

- б

а в

б г

в д

г

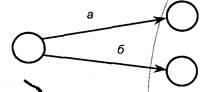
Построение модели: Работам а и б никакие работы не предшествуют. Работа в выполняется после работы а.

Работа г выполняется после работы б, работа в после работы а

Окончание работы в объединяется с окончанием работы г, так как следующая работа д должна выполняться после окончания работ в и г.

Важнейшим вопросом построения сетевого графика является четкое определение всех взаимосвязей между работами и их технологической последовательностью. При кодировании сетевых графиков необходимо учитывать следующие положения:

все события имеют самостоятельные номера;

кодируются события числами натурального ряда (без пропусков); номер последующему событию присваивается после присвоения но­меров предшествующим ему событиям;

работа должна быть всегда направлена от события с меньшим номе­ром к событию с большим номером.

Поток в сети направлен в одну сторону - всегда от начала к концу сети.

Сетевой график дает исполнителям ясное представление о взаимо­связи различных работ и позволяет предотвратить неправильное понима­ние ими ответственности, сокращает до минимума возможность упуще­ния в графике какой-либо части работ.

После того как план представлен в виде сетевого графика, присту­пают к составлению графика его выполнения при нормальной продолжи­тельности работ. Под нормальной продолжительностью работы понимается наименьшее время выполнения работы без каких- либо дополнительных расходов для ее ускорения. Над каждой стрел­кой записываются следующие данные: наименование работы, нормаль­ная продолжительность работы и ее стоимость, продолжительность при экстренном выполнении и ее стоимость. Под стрелкой указывается ко­личество людей по профессиям, подвижной состав или тип ПРМ.

Если концентрировать усилия на работах, которые находятся на критическом пути, и добиваться их своевременного выполнения, то про­ект будет завершен вовремя. Когда возникает необходимость ускорить работы при минимальных затратах, то для всех работ устанавливаются ранние и поздние сроки возможного начала и окончания (устанавли­вать сроки необходимо с применением теории вероятности). Необходимо стремиться не к максимально возможному, а к максимально целесооб­разному ускорению. Каждая работа имеет определенный предел уско­рения. Если выполнение работы затягивается, то это ведет к беспо­лезному увеличению затрат.

Время выполнения работ будет колебаться в пределах от нормальной до экстремальной продолжительности. Это означает, что имеется множе­ство путей - вариантов выполнения любого плана. Сетевые графики мо­гут быть ориентированы не только на критерий времени, но и на другие параметры, например, минимизацию ресурсов или конечной стоимости работ по выполнению заданного плана. Из этого множества необходимо выбрать оптимальный вариант. Чаще всего критерием выбора служат минимальные затраты при заданной продолжительности.

Сетевой график может быть выполнен с различной степенью дета­лизации процесса. Для разных уровней управления степень детализации или укрупнения сетевых графиков может быть различной.

При календарном планировании необходимо учитывать ограничения денежных средств, а главным образом ресурсов (рабочая сила, подвиж­ной состав, погрузочно-разгрузочные средства). Без этого учета со­ставленные планы могут оказаться нереальными. На транспорте работни­ки одних профессий имеют основной целью обеспечение деятельности работников других ведущих профессий. Следовательно, наличие работ­ников ведущих профессий (водителей на линии) зависит от наличия ра­ботников вспомогательных профессий (ремонтных и обслуживающих). Перевозки неравномерно распределяются по времени года и дням месяца (в одном месяце 200 водителей, в другом - 150). Для улучшения исполь­зования рабочей силы и подвижного состава определяется, какие из вы­полняемых в пиковый период работ имеют свободный резерв времени и когда их можно выполнять за пределами пикового периода и так далее до получения приемлемого решения.

Следующей ступенью совершенствования сетевых моделей является создание сетевых матриц. Сетевая матрица, описывая графиче­ски отдельные технологически взаимосвязанные операции и их конкрет­ные промежуточные цели - результаты, позволяет прогнозировать дос­тижение промежуточных и конечных результатов, глубже анализировать значение и место каждой отдельной операции в общем комплексе проце­дур, направленных на достижение предполагаемой цели, и на этой основе сформировать план выработки и реализации решения.

Сетевая матрица решений представляет собой се­тевой график совмещенных с календарно-масштабной сеткой времени, которая имеет горизонтальные и вертикальные «коридоры». Горизон­тальные «коридоры» характеризуют ступень управления, структурное подразделение или должностное лицо, выполняющее ту или иную опера­цию процесса подготовки, принятия и реализации решения. Вертикаль­ные «коридоры» характеризуют этап и отдельные операции процесса принятия решения, протекающие во времени.

Построение сетевых матриц. Принадлежность работы к тому или иному горизонтальному «коридору» определяется ее гори­зонтальным положением, а принадлежность к вертикальному «коридо­ру» - вертикальными линиями, определяющими масштаб времени мат­рицы.

Из рис. 8.16 видно, что работы а и б выполняются начальником АТП, работы в и г - заместителем начальника, работы д - главным инженером. Работы а и в выполняются на 1 этапе решения; работы б и г - на втором этапе, а работы д - в течение первого и второго этапов. Продолжитель­ность каждой работы на сетевой матрице определяется расстоянием по сплошной линии между центрами двух событий, заключающих эту ра­боту в проекции на горизонтальную ось времени. В нашем примере работы а не имеют продолжительность, равную четырем единицам времени. Все остальные работы, заканчивающиеся раньше, но входящие в это событие, соединяются с ним волнистой линией со стрелкой на кон­це.

Длина волнистой линии показывает величину частного резерва вре­мени. Например, работа г имеет частный резерв во времени, равный двум временным единицам.

8.9. СИТУАЦИОННЫЕ ИГРЫ

В слово «игра» вкладывается много значений: спортивные игры, во­енные тренировки, искусство (особенно его исполнительные формы). Игры имеют важное значение в воспитании, обучении и развитии де­тей, выступая как средство психологической подготовки к будущим жизненным ситуациям. В общем случае игра - вид непродук­тивной деятельности, мотив которой заключается не в ее результатах, а в самом процессе.

Игра может выступать как разновидность общественной практики, состоящая в воспроизведении (моделировании) жизненных явлений, в которых участники ставят прямо противоположные задачи и добива­ются осуществления своих целей различными путями. Играть в эко­номике - предпринимать действия, которые могут повлечь за собой серьезные последствия.

Теория игр - раздел математики, в котором изучаются матема­тические модели принятия оптимальных решений в условиях конфликта, т. е. при явлении, в котором участвуют различные стороны, наделен­ные различными возможностями выбирать для них действия, в соответ­ствии с их интересами. Схемы теории игр охватывают как собственно иг­ры (шахматы, домино), так и различные ситуации, возникающие в эко­номических, военных и других вопросах.

Современная теория игр связана с именем крупнейшего математика американца венгерского происхождения Джона фон Неймана. Теория игр развивалась на основе изучения салонных игр, в частности, игры в по­кер. Такие игры, как, в рулетку или в кости, являются в отличие от покера не стратегическими, а механическими, в которых чистая случайность исхода каждой игры обеспечивает в силу законов теории вероятностей устойчивый доход игорному предприятию. Доказано, что не существует стратегии, использовав которую игрок мог бы выиграть в достаточно длинной серии партий. Однако, в течение недолгого вре­мени результаты могут сложиться в пользу игрока.

Игры классифицируются: по числу игроков, по сумме выигрыша и проигрыша, на коалиционные (кооперативные) и бескоалиционные (не­кооперативные), с полной информацией (в которых все участники распо­лагают полной информацией о сложившейся в игре ситуации в каждый момент времени) и с неполной информацией (в которых участники рас­полагают неполной информацией о позициях, сложившихся в игре).

По числу игроков все игры делятся на три вида: с одним, двумя, тре­мя или большим числом участников.

Если игрок один, то он играет против природы. Он не должен беспо­коиться, что его противник (природа) свободно принимает решения по­добно ему самому. Если идет дождь, то он идет независимо от «желания» природы. Но игрок вычисляет, сколько миллиметров осадков выпало в году, в какое время года и каковы шансы или вероятность того, что сно­ва будет дождь. Это игра случая, изучаемая методами теории вероятно­стей.

Наличие двух участников является минимально необходимым условием возникновения отношений людей и их взаимодействия. Если в игре участвуют три или большее число игроков, они могут обра­зовывать группы или коалиции. Обозначим через J множество всех игро­ков. Обычно принято различать игроков по их номерам, т. е. считать, что J = {l, 2,..., п). Каждый игрок i € J имеет в своем распоряжении не­которое множество S_i возможных действий, которые в теории игр назы­ваются стратегиями. Естественно считать, что каждый игрок имеет не менее двух различных стратегий. Если он располагает только одной стра­тегией, его действия оказываются заранее определенными, и он фактиче­ски в игре участия не принимает.

Процесс игры состоит в выборе каждым из игроков одной своей стратегии S. Таким образом, в результате каждой партии игры складыва­ется система стратегий

которая называется ситуацией. Множество всех ситуаций обо­значается

В каждой ситуации S игроки получают некоторые выигрыши.

Если игрок выбирает бескоалиционную игру, то тем самым он прини­мает одностороннюю точку зрения на перспективные взаимодействия. Он изучает используемые стратегии, ищет способы независимого пове­дения, приводящие к наилучшим результатам при любых действиях ос­тальных участников игры.

Если он избирает коалиционный вариант и может вступать в коали­ции, то он попытается определить предпочтительность участия в воз­можных коалициях по сравнению с ценностью игры в одиночку. В кар­точных играх, обычно, игра ведется бескоалиционно. Политические игры - коалиционные. Экономические игры могут протекать по-разному, в зависимости от их правил, размеров ожидаемых выигрышей и наклонностей игроков.

Для игры характерна неопределенность. Различают два вида неопределенности: случайность и выбор. Сколько очков выпадет на иг­ральной кости - совершенно иной вопрос, чем как может поступить иг­рок, если у него есть возможность выбора стратегии. В классическом по­кере имеются как случайности (при раздаче карт), так и выбор страте­гии. Каждый игрок может повысить цену игры, но при этом совершенно неясна сила комбинации его карт, поскольку он их не показывает. Мно­гие салонные игры имеют элементы случайности и дают возможность выбора. Большинство игр в реальной жизни также содержат оба вида не­определенности. Если предприниматель повысит или снизит цену, то во­прос о том, последует ли за ним конкурент, является стратегическим: конкурент может выбирать.

Различие между неопределенностью случая и выбором - важный момент в теории игр. Это приводит к выделению двух видов игроков: стратегических и нестратегических. Стратегический игрок имеет свободу выбора; нестратегический игрок не имеет дру­гой возможности, кроме как принять или отказаться от чего-либо. Он участвует в игре и может получить выигрыш. В экономических играх ти­пичными нестратёгическими игроками являются потребители, мелкие акционеры и т. д. Стратегические игроки, как правило, занимают ре­шающие позиции при заключении сделок.

Если два лица ведут игру с нулевой суммой типа шахмат и так далее, то условия требуют независимых действий каждого, так как интересы этих игроков полностью противоположны. Они не могут образовывать коалицию. В игре трех участников с нулевой суммой их интересы проти­воположны, но не полностью. Любые два игрока могут объединиться в коалицию против третьего, как это часто бывает в политических играх.

Если два лица (например, покупатель и продавец) ведут игру не с ну­левой суммой, то они имеют как общие, так и противоположные интере­сы. Общие - желание получить взаимную выгоду. Противоположные ин­тересы - как ее поделить.

Правила игры - это абсолютные, не подлежащие обсуждению предписания. На практике правила игры можно критиковать и просто на­рушать. Изменение правил - изменение самой игры. Существование игры подразумевает согласие участников с ее правилами. Игра состоит из последовательности ходов, а партия игры - из последовательности выборов. В ходе игры за каждым выбором, т. е. ходом, одного игрока следует выбор, или ход другого из числа имеющихся в его распоряжении возможностей. В некоторой точке игра прекращается, и оценивается ее результат.

Правила игр, развертывающихся в человеческой деятельности, менее точны, чем те, в которые играют люди, а тем более, чем правила абст­рактных игр теоретиков.

В настоящее время в литературе встречаются много названий игр

- деловые, операционные, ситуационные, транспортные и др. Классиче­ским примером деловой игры может служить игра между фирмами «Форд» и «Дженерал моторс».

В 1921 г. фирма «Дженерал моторс» разработала модель игры между «Дженерал моторсом» и «Фордом». Цель - захват рынка дешевых авто­мобилей, который тогда полностью заполнил «Форд» своими знамени­тыми автомобилями - «Моделью-Т». Корпорации, участвовавшие в этой игре, в настоящее время выглядят так - «Дженерал моторс» произво­дит более половины автомобилей США, «Форд» - около трети. В 1921 г. это соотношение было иным. «Форд» производил более половины всех автомобилей, «Дженерал моторе» - десятую часть. Следует отметить, что «экономическая сила» корпораций была примерно одинакова (сумма продаж). «Форд» производил единственный вид дешевого автомобиля - «Модель-Т», а «Дженерал моторс» - несколько, от «Шевроле» - сред­ней цены до «Кадиллака» - очень дорогого автомобиля. До 1921 г. «Дже­нерал моторе» не контактировала на рынке с «Фордом» и решила покон­чить с монополией «Форда» на рынке дешевых автомобилей.

Форд был самым выдающимся, в то время, бизнесменом в мире. Он был героем публики: платил высокую зарплату и дешево продавал авто­мобили. Его автомобиль стоил 415 долларов. Он продавал в год около 2 млн. автомобилей. При большом объеме производства он значительно снизил себестоимость производства и продавал автомобиль по самой низкой цене. Когда другой автомобиль приближался по цене к «Модели- Т», Форд еще более снижал цену. Никто не мог выдержать такой игры.

Форд рассматривал «Модель-Т» как «вечную» и не принимал мер к разработке другой модели.

Корпорация «Дженерал моторс» разработала модель всего рынка автомобилей, разделив его на 6 стоимостных групп: первый класс - от 450 до 600 долларов, второй - от 600 до 900, третий - от 900 до 1200, четвертый - от 1200 до 1700, пятый - от 1700 до 2500 и шестой - от 2500 до 3500 долларов. Эксперты фирмы отвергли предложение производить и продавать автомобили по цене «Форда». Они предложили спроектиро­вать и поставить на рынок значительно лучший автомобиль по цене, максимальной для автомобилей первого класса или близкой к ней. По их мнению, такой автомобиль должен был изменить спрос на автомобили второго класса (покупатели, экономя 150 долларов, могут поступиться сравнительно небольшими преимуществами автомобиля более высокого класса). «Дженерал моторс» сформулировала свою основную цель: де­лать деньги, а не автомобили.

После принятия решения «Дженерал моторс» выпустила на рынок «Шевроле» с кузовом типа «фаэтон» за 820 долларов, создав новую си­туацию в классе дешевых автомобилей. Форд продавал свои автомо­били по цене 415 долларов. Через несколько месяцев цена на «Шевро­ле» была снижена до 525 долларов, а на «Модель-Т» - до 355 долларов. «Дженерал моторс», продав за год около 70 тыс. автомобилей, теряла ежемесячно по миллиону долларов.

Форд понял, что ему брошен вызов и в 1922 г. снизил цену на свой ав­томобиль до 300 долларов. Однако «Дженерал моторе», продав в 1922 г. около 200 тыс. автомобилей и обеспечив себе тем самым безубыточное производство, решила цену на «Шевроле» не снижать. Таким образом, в 1922 г. Форд и «Дженерал моторе» поделили рынок дешевых автомо­билей. Форд получил 87 %, «Дженерал моторе» - 13 %.

В 1925 году упали цены на закрытые автомобили и соответственно увеличился на них спрос. Фирма «Дженерал моторс», учитывая это, разработала новую модель «Шевроле», которая могла использовать как от­крытый, так и закрытый автомобиль. Форд остался со старой моделью. В 1926 г. «Дженерал моторс» продала 700 тыс. автомобилей, причем три четверти из них были с закрытыми кузовами.

Завоевав достаточный объем, «Дженерал моторс» снизила цены на свои закрытые автомобили до уровня Форда, став с ним «на равных». Не найдя подходящего ответа и осознав свое поражение, Форд закрыл в 1927 г. свои заводы и приступил к проектированию новой модели, назвав ее «Моделью-А», которая появилась на рынок в 1928 г. За это время «Дженерал моторс» уже прочно закрепилась на рынке дешевых автомобилей.

В настоящее время игры находят широкое применение в разрешении ситуаций хозяйственного управления.

В управленческих играх основным понятием является имитация. Имитация начинается с составления описания данной организации и ее положения, достаточно полного и точного, чтобы позволить группе по­средников или ЭВМ определить логические методы принятых решений.

Всякая игра связана с исполнением ролей, так как участники должны «вжиться» в предписанную ситуацию. Игра содержит в себе ситуацион­ный и послеигровой анализ.

Ситуационный анализ имеет несколько разновидностей.

Участнику игры предлагают исполнить роль директора предприятия и предпринять требуемые действия в связи с полученной им корреспон­денцией (большим числом (не менее 10) писем, докладных записок или документов). Участнику требуется избрать определенный курс действий на основе данной информации. Руководитель игры или инструктор сооб­щает дополнительную информацию, только если ее запрашивают и др. Иг­ра сопровождается послеигровыми комментариями, а также обсуждениями и спорами, порождаемыми самой игрой.

В реальной жизни большинство решений принимается в условиях неполноты, неточности и неопределенности информации. В играх с ис­пользованием ЭВМ, по самой их природе, необходима более точная ин­формация. Ситуационный анализ также обычно дает точную, хотя и не­полную информацию. Поэтому играющие команды, имеющие различ­ные структуры и состав, по-разному воспринимают исходные данные и получают различные результаты.

На автомобильном транспорте игры применяются для решения воз­никающих ситуаций и прогнозирования производственных процессов, а также для повышения квалификации специалистов.

В настоящее время разработано несколько вариантов так называемой транспортной игры, цель которой заключается в прогнозировании пере­возочного процесса с учетом реально возникающих ситуаций при ор­ганизации перевозок.

В зависимости от поставленных задач игра может проводиться как с высокой, так с ограниченной достоверностью получаемых результа­тов. Игра должна воспроизводить модель действительности, упрощая или усложняя ее.

Однако моделирование реальных ситуаций даже в порядке экспери­мента позволяет ближе познакомиться с сущностью изучаемого процесса по мере развертывания игры, а также проверить собственное знание дела и уровень профессиональной подготовки играющих. Необходимо толь­ко, чтобы предварительное планирование игры было достаточно де­тальным, но при этом оставалась также значительная свобода для пере­стройки по ходу дела.

Игры, используемые как способ приобретения опыта управления, ставят своими задачами:

выработать у хозяйственных руководителей навыки в решении кон­кретных управленческих ситуаций, с которыми они постоянно сталкива­ются на практике;

совершенствовать навыки анализа, учить отделять нужное от не­нужного, определять первостепенные задачи, отличать факты от мне­ний, ставить реальные задачи, оценивать их;

совершенствовать навыки общения с людьми, свой стиль работы, по­ведение.

В подготовке и проведении таких игр участвуют все специалисты предприятия. Специалисты, проявившие себя в ситуационных играх, за­числяются в резерв на выдвижение.

Темы игр: совершенствование работы пассажирского транспорта, по­вышение эффективности управления и воспитательная работа, совершен­ствование работы грузового транспорта, развитие технической службы управления и др.

Процесс подготовки ситуационной игры разбивается на несколь­ко этапов. Прежде всего, определяется цель игры, затем - игровой ком­плекс: уровень, моделируемый в игре (служба, предприятие, объеди­нение), уровень комплексности (круг проблем, задач и их взаимо­связь).

Далее намечается структура игры: число команд и их задачи, пери­од подготовки и система предварительной оценки готовности, кон­сультанты, эксперты и т. д. После этого разрабатывается черновой вариант игры, в ходе которого определяются и уточняются ее правила и документы. Каждая игра предназначается для определенного звена управленческих работников.

Порядок проведения ситуационной (деловой) игры:

ввод в игру;

формирование групп (команд);

работа групп над темой;

контроль предварительной готовности;

процесс игры;

подведение итогов.

На этапе «ввод в игру» руководством предприятия определяется тема игры, формулируются цели и задачи, подбирается кандидатура на роль руководителя игры. Задачами играющего начальника предприятия стано­вятся: формирование играющего аппарата и подготовка сценария ситуа­ционной игры. Для написания сценария назначается группа компетент­ных специалистов.

Сценарий включает следующие разделы:

структура игры (количество команд и их задачи);

регламент игры (время и периодичность выступления команд, про­должительность этапов и перерывов и т. п.);

организационное обеспечение;

общая технология игры (выступления, оппонирование, работа с залом, заключительный этап и т. д.).

Процесс игры. Команда докладывает о том новом, что ею предлагает­ся для улучшения работы предприятия. Оппонент аргументированно со­глашается или не соглашается с их предложениями. При необходимости команда представляет свои контраргументы. Атмосфера игры, когда ру­ководитель службы один на один с играющей командой при полном за­ле слушателей анализирует результаты своей работы за ряд лет, обсу­ждает направления будущей деятельности, оказывается не для всех уютной. Некоторым приходится и краснеть, и открыто признавать свои промахи, и объективно оценивать рекомендации. В этой обстановке и проверяются личные качества руководителя и его соответствие должно­сти. Такая игра - хорошая проверка не только резерва на выдвижение, но и руководящих кадров предприятий.

Подведение итогов. Оценка и обсуждение игры проходят когда при­сутствуют все члены всех команд. Это позволяет выслушать всех игроков и оптимизировать процесс вовлечения участников, как в саму оценку, так и в возникающее понимание проблем. Итоги подводят члены арбитражной комиссии. Это, как правило, начальник предприятия, объединения и его заместители. Они обращают внимание всех присутствующих на наиболее интересные предложения команд, оценивают их работу и определяют лучших. На основе предложений играющих составляется план мероприя­тий, который утверждается руководством предприятия.

Подобные игры целесообразно проводить на всех предприятиях не менее одного раза в год.

ВЫВОДЫ

1. Проблема повышения эффективности перевозок грузов связана с широким применением методов классической и современной математики для решения прикладных задач. По своему характеру все решаемые на транспорте задачи делятся на три класса: разработка технологических процессов перевозки грузов; оперативное планирование и управление пе­ревозками; учет и статистика.

2. В настоящее время инженеру по организации перевозок и управле­нию на транспорте необходима математическая культура. Он должен иметь четкое представление о математическом аппарате решения организационно-управленческих задач и использования их на практике (уметь математически грамотно сформулировать задачу, составить математиче­скую модель, понимать технику расчетов и полученные результаты).

3. Разработка технологических процессов перевозки грузов связана с линейным программированием: с определением кратчайших расстояний между пунктами транспортной сети; составлением рациональных мар­шрутов при перевозке массовых грузов; с закреплением потребителей за поставщиками; с рациональным использованием различных моделей ав­томобилей на перевозках различных грузов и др.

При разработке технологических процессов перевозок грузов основ­ное внимание должно уделяться на формулировку задач и технику расче­тов (выбору критерия оптимальности, подготовке данных, технико-экономическому анализу полученных результатов, экономической ин­терпретации результатов решения).

4. Методы линейного программирования позволяют не только уста­новить последовательность действий для нахождения кратчайших путей получения оптимальных численных значений управляемых переменных, но и знать, в каком интервале можно менять входные параметры без су­щественного отклонения от найденного оптимума и без значительного нарушения структуры базиса, формирующего оптимальное решение.

5. Процесс автомобильных перевозок грузов представляет собой сис­тему массового обслуживания, для которой характерны следующие осо­бенности: моменты прибытия отдельных единиц подвижного состава в пункты погрузки-разгрузки, как правило не могут быть абсолютно точно предсказаны; длительность их обслуживания в этих пунктах сильно ме­няется как от вида перевозимых грузов, так и от размещения перевозок по времени; погрузочно-разгрузочные посты имеют не одинаковую за­грузку, и в результате сильно загруженные промежутки времени череду­ются с промежутками слабой загрузки. Поэтому возникающие потери от этих факторов могут быть предсказаны с помощью математического ап­парата теории массового обслуживания.

6. Математический аппарат теории вероятности и теории массового обслуживания широко используются в теории игр - разделе математики, в которых изучаются математические модели принятия оптимальных ре­шений в условиях конфликта.!

В реальной жизни большинство решений принимается в условиях неполноты, неточности и неопределенности информации. Поэтому моде­лирование возникающих ситуаций повышает достоверность протекания перевозочных процессов и способствует повышению их эффективности.

Вопросы для самоконтроля

1. Какие математические методы применяются в технологии, органи­зации и управлении автомобильными перевозками грузов?

2. Охарактеризуйте сущность методов линейного программирования.

3. Сущность графоаналитического метода.

4. Какие критерии оптимизации применяются при решении классиче­ской транспортной задачи?

5. Какие вы знаете способы составления базисного плана? Сущность способа аппроксимации У. Фогеля?

6. Требования предъявляемые к базисному плану?

7. Решение транспортной задачи. Сущность метода потенциалов.

8. Какие дополнительные условия учитываются при решении транс­портных задач?

9. Решение транспортной задачи в сетевой форме.

10. Методы оптимизации транспортной задачи (метод потенциалов, метод Хичкока, метод Креко).

11. Какие признаки указывают на наличие альтернативных решений при различных методах оптимизации транспортной задачи?

12. Решение открытых моделей транспортной задачи.

13. Методы решения задач маршрутизации мелкопартионных перево­зок.

14. Решение задач маршрутизации домашинных отправок. Метод со­вмещенной матрицы.

15. Основные правила при решении задач симплексным методом.

16. Вычислительная процедура симплексного метода.

17. Определение исходного базиса при решении задач симплексным методом.

18. Анализ модели на «чувствительность»

19. Сущность двойственности задач линейного программирования.

20. Применение теории массового обслуживания при прогнозирова­нии технологических процессов перевозок массовых грузов.

21. Какие основные правила применяются при построении сетевых графиков?

22. Назовите основные понятия при разработке сетевых моделей.

23. Классификация ситуационных игр и их использование на транс­порте.

Глава 9

Не нашли, что искали? Воспользуйтесь поиском: