ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Резонансные режимы работы двухполюсника.
Пусть двухполюсник содержит один или несколько индуктивных элементов и один или несколько конденсаторов.
Резонансным режимом работы такого двухполюсника является такой режим, при котором входное сопротивление двухполюсника является чисто активным. Следовательно, для определения условий наступления резонанса необходимо приравнять к нулю мнимую часть комплекса входного сопротивления двухполюсника. Такой способ справедлив, если не пренебрегать активными сопротивлениями индуктивных катушек.
По отношению к внешней цепи двухполюсник в резонансном режиме ведет себя как активное сопротивление, поэтому ток и напряжение на его входе совпадают по фазе. Реактивная мощность двухполюсника при этом равна нулю.
Различают две основные разновидности резонансных режимов: резонанс токов и резонанс напряжений.
Резонанс токов называют я вление резонанса в схеме (рис. 3.15 а), об-разованной двумя параллельными ветвями с разнохарактерными реактивными сопротивлениями.
Пусть первая ветвь содержит активное сопротивление R1 и индуктивное ωL, а вторая ветвь - активное R2 и емкостное 1/ωС.
Ток 
в первой ветви отстает от напряжения 
(рис. 3.15, б) и может быть записан как
Рисунок 3.15
Ток I2 во второй ветви опережает апряжение:
Ток в неразветвленной части цепи
По определению резонансного режима ток I должен совпадать по фазе с напряжением U. Это будет при условии, что сумма реактивных проводимостей ветвей равна нулю: b1+ b2 =0.
Для данной схемы
Следовательно, условие наступления режима резонанса токов в схеме на рис. 3.15, а можно записать так:
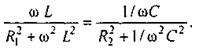(3.56)
На рис. 3.15 б изображена векторная диаграмма для резонансного режима. Из (3.56)следует, что если R2 = 0, то резонанс наступит при
(3.57)
В еще более частном случае, когда R2=0 и R1 «ωL, резонанс наступит при
(3.58)
Резонанса можно достичь изменением ω, L, С или R1 и R2. Числовое значение тока в неразветвленной части схемы может быть меньше токов в ветвях схемы. При R2 = 0, R1 ~ 0 ток I может оказаться ничтожно малым по сравнению с токами I1, и I2.
В идеализированном, практически не выполнимом режиме работы когда R1 = R2 = 0, ток в неразветвленной части схемы на рис. 3.15 а равен нулю и входное сопротивление равно бесконечности.
Обратим внимание на следующее. В формулу (3.56) входит пять величин (L, С, R1 R2, ω). Если определять из нее L или С, то может оказаться, что для искомой величины будут получены одно или два действительных значения либо мнимое значение.
Получение двух действительных значений для L и С свидетельствует о том, что при неизменных четырех параметрах вследствие изменения пятого можно получить два резонансных режима. Получение мнимых значений L и С свидетельствует о том, что при данных сочетаниях параметров резонанс невозможен.
Определим ω из (3.56):
(3.59)
где 
-резонансная частота в контуре без потерь при R1=R2= 0.
Поскольку угловая частота действительна и положительна, то числитель и знаменатель формулы (3.59) должны быть с одинаковыми знаками. Это имеет место при
При R1 = R2 частота ω = ω 0.
При 
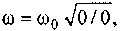
т. е. ω получается величиной неопределенной. Физически это означает, что резонанс может возникать при любой частоте. Сопротивление парал-лельного контура равно 
Входное сопротивление большинства потребителей электрической энергии имеет индуктивный характер. Для того чтобы уменьшить потребляемый ими ток за счет снижения его активной составляющей и тем снизить потери энергии в генераторе и подводящих проводах, параллельно приемнику энергии включают батарею конденсаторов.
Уменьшение сдвига фаз между напряжением на приемнике и током, потребляемым от генератора, называют компенсацией сдвига фаз.
Компенсация сдвига фаз существенна для энергоемких потребителей, например крупных заводов. Осуществляется она в месте ввода линии питания в распределительном устройстве. Экономически выгодно подключать конденсаторы на возможно более высокое напряжение (ток через конденсаторы Ic =U ωС). Сдвиг фаз ω между напряжением и током, потребляемым от источника питания, доводят до значения, при котором cosφ ~ 0,9 + 0,95.
Резонансом напряжений называют резонанс в схеме последовательного соединения R, L, С (рис. 3.16 а).
При резонансе ток в цепи должен совпадать по фазе с ЭДС Е. Это возможно, если входное сопротивление схемы Z = R + j (ωL-1/ωC) будет чисто активным. Условие наступления резонанса в схеме(рис. 3.16 а).
(3.61)
где ω0 - резонансная частота.
Рис.3.16
При этом 
. Модуль напряжения на индуктивном элементе при резонансе равен напряжению на емкостном элементе:
Отношение
(3.62)
Пусть в этой схеме параметры R, L, С и ЭДС E постоянны, а меняется частота ω. Рассмотрим характер изменений модулей тока I и напряжений UL и Uc в функции от ω.
Ток в цепи
При изменении ω меняется реактивное сопротивление цепи следующим образом:
при ω → 0 сопротивление X → ∞ и ток I → 0;
при 
сопротивление X = 0, ток I= E/R;
при ω → ∞ сопротивление X → ∞, ток I → 0.
Напряжение
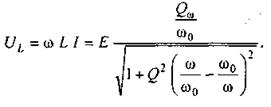
при ω → 0 напряжение UL= 0;
при ω → ∞ напряжение UL → E (рис. 3.16, в);
при ω → 0, 
при ω → ∞ напряжение Uс → 0.
Из рис. 3.16, в видно, что максимумы напряжений UL и Uc имеют место при частотах, не равных резонансной частоте 
:
максимум Ul имеет место при частоте ω L > ω 0, а максимум Uc - при частоте ω с < ω0.:
На рис. 3.16, г изображены две кривые, характеризующие зависимость I = f(ω) ля цепи с неизменными L, С и Е при двух различных значениях R. Для кривой 2 сопротивление R меньше (а добротность Q больше), чем для кривой 1.
Обычно кривые изображают в относительных единицах: ток в долях от тока при резонансе, частота - в долях от резонансной частоты. Графики тока в относительных единицах изображены на рис. 3.16 д. Они построены по формуле
Чем меньше активное сопротивление резонансного контура при неизменных остальных параметрах схемы, т. е. чем больше добротность контура Q, тем более острой (пикообразной) становится форма кривой I = f(ω).
Полосой пропускания резонансного контура называют полосу частот
ω2 – ω1 = ω0 / Q, на границах которой отношение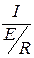 
составляет 0,707(рис. 3.16 д).
Граничные частоты 
. Аргумент входного сопротив-ления схемы (рис. 3.16, а) 
.
Если в данной схеме изменять не частоту, а индуктивность L, то за-висимости I, UL, в функции от ХL =ωL (со = const) будут иметь вид кривых рис. 3.16 е.
Не нашли, что искали? Воспользуйтесь поиском: