Резонанс в индуктивно связанных контурах.

Схема двух индуктивно связанных контуров приведена на рис. 3.30 а. Взаимная связь этих контуров определяется коэффициентом взаимной индукции М. Для определения входного сопротивления воспользуемся приведением вторичного контура к первичной Цепи при помощи вносимого сопротивления, как показано на рис. 3.30 б

(16.19)

где ^- полное комплексное сопротивление первого контура;

Z_вн = r_вн+jx_вн = -Z_М² /Z₂ - комплексное вносимое сопротивление (подробно рассмотренное в лекции 10);

r_вн - активное вносимое сопротивление;

x_вн = - x_М²/x₂ - реактивное вносимое сопротивление;

х_м = ωМ - сопротивление взаимной индукции;

x₂ = x_L2 - х_С2 - реактивное сопротивление вторичного контура.

Рис.3.30.

После подстановки в формулу (16.19) значения вносимого реактивного сопротивления х_вн запишем условие резонанса в цепи

откуда получаем

(16.20)

Из формулы (16.20) следует, что резонанс в индуктивно связанной цепи наступает при выполнении условия

(16.21)

Если использовать коэффициент связи и положить, что резонансные частоты контуров одинаковы ω₁ = ω₂ = ω₀ или L₁C₁. = L₂C₂, то уравнение (16.21) можно записать в виде:

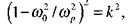(16.22)

откуда получаем, что

Из этого уравнения находим значения резонансных частот индуктивно свя­занных контуров

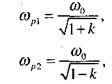(16.23)

где 0 < k < 1.

Выполненное рассмотрение показывает, что система индуктивно связанных контуров имеет две резонансные частоты, одна из которых ω_р1 ниже, другая ω_p2 выше частоты ω₀. Это явление является очень важным свойством индуктивно связанных контуров. Эти резонансные частоты зависят от коэффициента связи и их обычно называют частотами связи. Расстояние между частотами ω_р1 и ω_p2 увеличивается с увеличением коэффициента связи k.

Внешний вид резонансных характеристик индуктивно связанных контуров показан на рис. 3.31. На этих резонансных характеристиках отчетливо видны два «горба», соответствующие резонансным частотам. При уменьшении k резонансные частоты сближаются и при k = 1/Q резонансная характеристика контура становится одногорбой.

Рис.3.31

Не нашли, что искали? Воспользуйтесь поиском: