Разработка алгоритмов и программ нисходящим способом

Разработать алгоритм и программу нисходящим способом, предполагая заданной матрицу A из 5 строк и 5 столбцов или одномерные массивы указанной длины.

1.	Даны две последовательности: C1,C2,...,C7; P1,P2,...,P7. Если каждый элемент первой последовательности меньше суммы элементов второй, найти при каких значениях i, j максимально значение выражения Ci / (Pj + Ci2).
2.	Если исходная последовательность C1,C2,...,C10 не содержит ни одного элемента, значение которого совпадает со значением какого-либо элемента последовательности P1,P2,...,P10, задать значения элементам X1,X2,...,X10 по правилу Xi = max(Ci, Pi)
3.	Даны две последовательности: С1,С2,...,С10; P1,P2,...,P10. Если наибольший элемент первой последовательности меньше наименьшего элемента второй, задать элементам X1, X2,...,X10 новой последовательности значения C1,C2,...,C10, а элементам X11,X12,...,X20 значения P1,P2,...,P10.
4.	Даны три последовательности: X1,X2,...,X6; Y1,Y2,...,Y6 и M1,M2,...,M6. Каждая тройка элементов (Xi, Yi, Mi) представляет параметры одной из шести материальных точек, лежащих в плоскости XOY; абсциссу Xi, ординату Yi и массу Mi. Если абсциссы и ординаты всех точек положительны, найти координаты центра тяжести данной ситстемы масс по формулам: ; .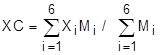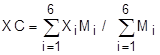
5.	Дана матрица P с двумя строками и десятью столбцами, каждым столбцом которой задана абсцисса и ордината одной из десяти точек плоскости. Если нет ни одной пары точек, расстояние между которыми меньше заданной величины R, заменить на нуль в матрице P все отрицательные абсциссы точек, увеличив ординаты этих точек на R.
6.	Если среднее арифметическое матрицы A положительно, задать элементам C1,C2,...,Ci значения тех элементов матрицы A, которые больше этого среднего арифметического.
7.	Если наибольший элемент матрицы A находится выше главной диагонали, найти сумму элементов матрицы, лежащих ниже главной диагонали.
8.	Найти среднее арифметическое элементов матрицы A, и, если матрица A не содержит ни одного отрицательного элемента, изменить элементы матрицы путем вычитания из них среднего арифметического.
9.	Если все элементы главной диагонали матрицы A отрицательны, разделить все элементы матрицы на максимальный по абсолютной величине элемент матрицы.
10.	Если разность максимального и минимального элемента матрицы A превышает заданную величину P, заменить в матрице A все отрицательные элементы нулями, а положительные единицами.
11.	Если среднее арифметическое элементов C1,C2,...,C7 больше минимального элемента матрицы, уменьшить на величину последнего каждый из элементов C1,C2,...,C7.
12.	Если сумма двух первых строк матрицы A меньше суммы элементов двух последних ее строк, изменить матрицу A, прибавив к элементам каждой строки заданные элементы X1,X2,...,X5.
13.	Если ни один из столбцов матрицы A, не содержит два и более равных нулю элемента, найти сумму элементов матрицы, лежащих на главной диагонали и выше нее.
14.	Если ниже главной диагонали матрицы A нет ни одного отрицательного элемента, изменить матрицу A, умножив каждый ее элемент на находящийся с ним в одной строке элемент главной диагонали.
15.	Если число отрицательных элементов матрицы A превышает число положительных, увеличить каждый элемент матрицы A на величину среднего арифметического всех ее элементов.
16.	Если сумма элементов последнего столбца матрицы A положительна, присвоить каждому из элементов X1,X2,...,X5 значение среднего арифметического соответствующей по номеру строки матрицы.
17.	Кроме матрицы A даны элементы C1,C2,...,C5. Если для всех Ci выполняется неравенство Ci > Aii, заменить значение каждого элемента Ci значением минимального элемента i-ой строки матрицы A.
18.	Если в матрице A элементы, равные нулю, встречаются не более, чем в двух строках, задать элементам X1,X2,...,X5 значения соответствующих по номеру элементов главной диагонали.
19.	Кроме матрицы A, даны элементы C1,C2,...,C5. Если значения всех этих элементов заключены между заданными значениями P и T, получить значения элементов X1,X2,..., X5 по формуле .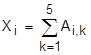
20.	Кроме матрицы A заданы элементы C1,C2,...,C5. Если среднее арифметическое CA элементов главной диагонали матрицы A меньше каждого из элементов C1,C2,...,C5, изменить матрицу A увеличением положительных ее элементов на величину CA и уменьшением отрицательных элементов на эту же величину.
21.	Если сумма Q положительных элементов матрицы A, превышает абсолютную величину суммы отрицательных из элементов C1,C2,...,C7, увеличить на Q значение каждого из этих элементов.
22.	Если в последовательности C1,C2,...,C5 имеются равные элементы, изменить значения всех ее элементов по правилу: Ci = Ci + Aii.
23.	Кроме матрицы A дана матрица B такого же размера. Если каждый элемент матрицы A больше соответствующего элемента матрицы B, присвоить элементам C1,C2,...,C5 значения по правилу .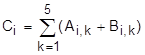
24.	Если среднее арифметическое каждого столбца матрицы A меньше заданной величины T, заменить значение каждого элемента матрицы A квадратом этого значения.
25.	Кроме матрицы A, даны элементы последовательности B1, B2,...,B5. Если для каждой строки матрицы A сумма ее элементов (Pi) меньше соответствующего элемента последовательности (Bi), присвоить всем элементам последовательности значения по правилу: Bi = Pi.
26.	Если разность максимального и минимального элементов каждой строки матрицы A не превышает заданной величины R, присвоить каждому из элементов C1,C2,...,C5 значение соответствующего по номеру элемента главной диагонали матрицы A.
27.	Если максимальный элемент матрицы A лежит на главной диагонали, присвоить начальным элементам последовательности C1,C2,...,C25 значения элементов матрицы, лежащих выше главной диагонали, а остальным элементам этой последовательности - значения прочих элементов матрицы.
28.	Если в матрице A нет элементов, абсолютная величина которых отличается от заданной величины P менее, чем на заданную величину E, найти для каждой ее строки среднее арифметическое положительных элементов.
29.	Кроме матрицы A дана матрица B такого же размера. Если для всех i,j выполняется неравенство Aij + Bij > 0, заменить значение каждого элемента матрицы A, который меньше соответствующего элемента матрицы B, значением этого элемента матрицы B.
30.	Если C5 > C4 > C3 > C2 > C1, где Ci - сумма элементов i-ой строки матрицы A, задать элементам i-ой строки матрицы значения соответствующих элементов (i+1)-ой строки, а элементам пятой строки задать значения элементов первой строки.

Не нашли, что искали? Воспользуйтесь поиском: