
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задача на использование формальных массивов в процедурах
Составить программу, содержащую процедуру, сходными данными которой является: матрица А из n строк и n столбцов, либо два массива B1,B2,...,Вn; C1,C2,...,Cm, либо один из них.
| 1. | Коэффициенты многочлена, являющегося суммой многочленов B1Xn+B2Xn-1+...+BnX; C1Xm+C2Xm-1+...+CmX. |
| 2. | Массив P1,P2,...,Pm, получаемый из C1,C2,..,Cm по правилу: заменить на 0 все элементы до первого отрицательного, который заменить на 1, а все остальные элементы заменить их модулями. |
| 3. | Множество значений, которые имеются и в массиве B1,B2,..., Bn, и в массиве C1,C2,...,Cm. |
| 4. | Номера всех элементов массива В1,В2,...,Bn, которые имеют наибольшее значение (оно может повторяться). |
| 5. | Массив D1,D2,...,Dm такой, что D1=Cm, D2=Cm‑1,..., Dm=C1. |
| 6. | Коэффициенты 1-й производной многочлена C1Xm + C2Xm-1 +... + CmX. |
| 7. | Значения трех наибольших элементов среди C1,C2,...,Cm. |
| 8. | Наибольший среди отрицательных элементов B1,B2,...,Bn и среднее арифметическое всех элементов. |
| 9. | Расстояния между 1-ой точкой двумерного пространства и всеми прочими точками, каждая из которых задана парой координат (Bi;Ci), i=1,2,...,n; n=m. |
| 10. | Массив, полученный перемещением отрицательных элементов массива C1,C2,...,Cm в его начало, а остальных - в его конец. |
| 11. | Массив P1,P2,...,Pm, полученный из массива C1,C2,...,Cm по правилу Pk 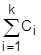 , k=1,2,...,m. , k=1,2,...,m.
|
| 12. | Множество всех значений, имеющихся в массивах B1,B2,..., Bn; C1,C2,...,Cm, без повторения значений. |
| 13. | Массив P1,P2,...,Pm, полученный заменой нулей в массиве C1,C2,...,Cm полусуммой соседних элементов (прочие элементы не изменяются); если 0 стоит на первом или последнем месте, то он заменяется значением соседнего элемента. |
| 14. | Массив элементов, каждый из которых встречается в массиве B1,B2,...,Bn не более 1-го раза. |
| 15. | Массив, каждый элемент которого равен наибольшему из двух элементов с таким же номером в исходных массивах (n=m). |
| 16. | Измененный массив C1,C2,...,Cm: каждый элемент, предшествующий минимальному, помножен на него, а все следующие за минимальным уменьшены на 1. |
| 17. | Массив P1,P2,...,Pn; Pi= 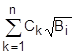 . .
|
| 18. | Номера элементов - локальных минимумов в массиве С1, C2,...,Cm и их количество. |
| 19. | Значения наименьших элементов строк матрицы A. |
| 20. | Средние арифметические значения:--элементов первого столбца матрицы А;-совокупности элементов 1-го и 2-го столбцов матрицы А; --совокупности элементов трех первых столбцов матрицы А. |
| 21. | Значение наибольшего элемента 1-й строки матрицы А, наименьшего элемента 2-й строки и среднее арифметическое всех элементов матрицы. |
| 22. | Массив P1,P2,...,Pn. Pi =1, если в i-й строке матрицы А положительных элементов больше, чем отрицательных, иначе Рi=0. |
| 23. | Суммы элементов, расположенных на главной диагонали матрицы А и всех нижележащих диагоналях (отдельная сумма для каждой из диагоналей), на главной диагонали номер строки равен номеру столбца. |
| 24. | Количество и координаты (номер строки и столбца) локальных минимумов матрицы А - элементов Аij, удовлетворяющих одновременно следующим неравенствам: Aij‑1 > Aij<Aij+1 и Ai-1j > Aij < Ai+1j. |
| 25. | Массив P1,P2,...,Pn; Pi=0, если i-ый столбец матрицы А не содержит элементов, абсолютная величина которых больше 1, иначе Рi=1. |
| 26. | Значения наименьших элементов во всевозможных квадратах матрицы А, левый верхний угол которых совпадает с элементом А11. |
| 27. | Новое содержание матрицы А, полученное замещением 1-й строки 2-й строкой, 2-й строки - 3-й строкой и т.д., в последней строке должно оказаться исходное содержание 1-й строки. |
| 28. | Множество элементов матрицы А - натуральных чисел, являющихся простыми числами (не делятся на меньшие натуральные, кроме 1). |
| 29. | Матрица D, каждый элемент которой Dij (i=1,2,...,n); (j=1,2,...,m) равен  . .
|
| 30. | Массив P1,P2,...,Pn; Pi(i=1,2,...,n) равен 1, если в i-й строке матрицы A нет элементов, которые меньше полусуммы максимального и минимального элементов матрицы, иначе Pi=0. |
Не нашли, что искали? Воспользуйтесь поиском: