Построение топографических диаграмм

Напряжений и векторных диаграмм

Токов

Каждая точка электрической схемы, в которой соединяются активные сопро­тивления, индуктивности, ёмкости, источники э.д.с. и тока имеет свое значение комплексного потенциала.

Совокупность точек комплексной плоскости, изображающих комп­лексные потенциалы одноимённых точек электрической схемы и соединённых между собой векторами, назы­вают топографической диаграммой напряжений.

Совокупность векторов, построенных из начала координат комплексной плоскости, концы которых имеют значения координат, рассчитанных токов, называют векторной диаграммой токов.

Последовательную схему рассмотрим на конкретном примере (рис.3.7).

Пример 7. Допустим R₁ = 7 [Ом]; X_L = 20 [Ом]; R₂ = 3 [Ом]; X_C = 10 [Ом]; e(t) = 311,1 Sin (1000 t +30^о) [B]. Определить ток , комплексы потенциалов точек схемы и построить топографическую диаграмму напряжений и векторную диаграмму токов.

Расчёт проведём в действующих значениях, поэтому сначала определяем действующее значение э.д.с.:

Так как начальная фаза равна 30^о, комплекс э.д.с. будет равен

Комплек с полного сопротивления контура

Ток в контуре по закону Ома равен

.

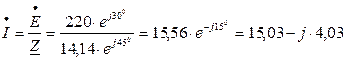Комплексы потенциалов точек схемы:

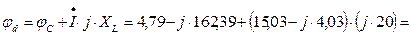
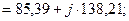
Схема содержит один контур, следовательно векторная диаграмма токов будет состоять из одного тока .

Потенциал точки е должен быть равен э.д.с. (второй закон Кирхгофа в комплексной форме), что и получено в результате расчёта. На рис.3.8 приведена топографическая диаграмма напряжений и векторная диаграмма токов, построенная по рассчитанным выше комплексам потенциалов точек схемы и комплексу тока. Из диаграммы видно, что напряжение U_ab = U_C перпендикулярно вектору тока I (вектор I построен в другом масштабе) и направлено в сторону отставания (по часовой стрелке), напряжения U_bc = U_R2 и U_de = U_R1 совпадают по направлению с током I, а напряжение U_сd = U_L перпендикулярно вектору тока I и направлено в сторону опережения (против часовой стрелки). Вектор э.д.с. Е =U_ae равен сумме векторов U_ab + U_bc + U_сd + U_de.

Рассмотрим цепь, состоящую из параллельного соединения индуктивности L и активного сопротивления R (рис.3.9, а). Допустим амперметры А₁ и А₂ имеют одинаковые показания 10 [А]. Требуется определить показание амперметра А₃. Считаем, что сопротивления амперметров равны нулю. Решение проведём с помощью векторной диаграммы токов. Зададим произвольно (предполо-жим по действительной оси) направление вектора напряжения U_ab. Вектор тока I₁ направлен перпендикулярно вектору напряжения U_ab в сторону отставания. Вектор тока I₂ совпадает с направлением вектора напряжения U_ab. Вектор тока I₃ является векторной суммой I₁ и I₂, а его длина определяется по теореме Пифагора

.

Для более сложных схем, состоящих из двух и более контуров можно применять метод узловых потенциалов, контурных токов, двух узлов и т.п. Однако, при ручном счёте на микрокалькуляторе требуется много времени. При использовании MathCAD время затрачивается только на расчёт комплексов сопротивлений ветвей и составление соответствующих матриц (см. п.2.5).

Пример 8. Рассчитать токи в ветвях схемы (рис.3.10) матричным методом, если e₁(t) =141,4 Sin( 314 t+ 45⁰ ); e₂(t) =169,7 Sin 314 t; Z ₁ =6–j6,5; Z ₂ =6+j5,08; Z ₃ =3,5+j4,96.

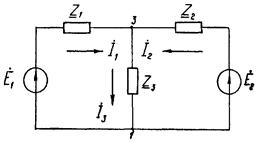Комплексы э.д.с. в действующих значениях:

;

.

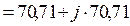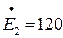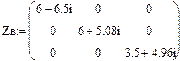
Составляем матрицы контуров В, источников э.д.с. Е в, источников тока J в и сопротивлений Z в:

Вычисляем матрицы контурных сопротивлений Z k, контурных э.д.с. E k и токов ветвей:

Комплексы токов:

;

;

или в мгновенных значениях:

;

;

.

3.5. Активная, реактивная и полная мощности

Под активной мощностью Р понимают среднее за период значение мгновенной мощности р. Если ток , апряжение на участке цепи , то активная мощность:

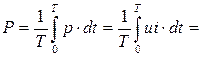
. (3.13)

Активная мощность физически представляет собой энергию, кото­рая выделяется в единицу времени в виде теплоты на участке цепи в сопротивлении R.. Действительно, 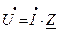, с другой стороны 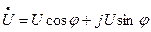или , следовательно, произведение U cos j = IR, а активная мощность

[Вт]. (3.14)

Под реактивной мощностью Q понимают произведение напряжения U на участке цепи на ток I по этому участку и на синус угла j между напряжением U и током I:

[ВАр]. (3.15)

Реактивную мощность принято измерять в вольтамперах реактив­ных [ВАр]. Если sin j > 0, то и Q > 0, если sin j < 0, то Q < 0. Под реактивной мощностью понимают скорость энергообмена между источником и реактивным элементом.

Полная (кажущаяся) мощность

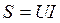[ВА] (3.16)

Между P, Q и S cуществует соотношение

. (3.17)

Рассмотрим простой приём определения активной и реактивной мощностей через комплекс напряжения и сопряженный комплекс тока. Напряжение на некотором участке цепи обозначим через 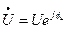, ток по этому участку . Угол между напряжением и током . Умножим комплекс напряжения на сопряжённый комплекс тока 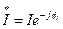и обозначим полученный комплекс через :

.

(3.18)

3.6. Двухполюсник в цепи синусоидального тока,

Не нашли, что искали? Воспользуйтесь поиском: