Резонансные режимы его работы

⇐ Предыдущая 8 9 10 11 12 13 141516 17 Следующая ⇒

Входное сопротивление двухполюсника (рис.1.1, б) при синусоидальном токе

. (3.19)

Если Х_ВХ > 0, то входное сопротивление имеет индуктивный характер, если Х_ВХ < 0 – ёмкостный, а если Х_ВХ = 0 – чисто активный.

Входная проводимость Y _BX представляет собой величину, обратную входному сопротивлению:

, (3.20)

где G_BX и B_BX – соответственно активная и реактивная входная проводимость.

Если Х_ВХ > 0, то В_ВХ >0, а если Х_ВХ < 0, то В_ВХ <0.

Пусть двухполюсник содержит одну или несколько индуктивностей и одну или несколько ёмкостей. Режим (или режимы), при котором входное сопротивление двухполюсника является чисто активным, называется резонансным.

По отношению к внешней цепи двухполюсник в резонансном режиме имеет активное сопротивление, поэтому ток и напряжение на входе двухполюсника совпадают по фазе.

Реактивная мощность двухполюсника при этом равна нулю.

Различают две основные разновидности резонансных режимов: резонанс токов и резонанс напряжений.

Явление резонанса в схеме рис.3.11, а, образованной двумя параллельными ветвями с разнохарактерными реактивными сопротивлениями, называют резонансом токов.

Пусть первая ветвь имеет активное сопротивление R₁ и индуктивное X_L, а вторая ветвь — активное R₂ и ёмкостное X_C.

Ток I₁ первой ветви (ветви с индуктивностью) отстает от напряжения U = U_ab (рис.3.11, б) и может быть записан так:

.

Ток I₂ второй ветви (ветви с ёмкостью) опережает напряжение U:

.

По первому закону Кирхгофа ток I в неразветвлённой части цепи

По определению резонансного режима, ток I должен совпадать по фазе с напряжением U. Это будет при условии, что сумма реактивных проводимостей ветвей равна нулю:

.

В соответствии с (3.20)

и

.

Следовательно, условие наступления режима резонанса токов в схеме рис.3.11, а можно записать так:

. (3.21)

На рис.3.11, б изображена векторная диаграмма токов для резонансного режима. Из (3.21) следует, что, если R₂ = 0, резонанс наступит при условии

.

В еще более частном случае, когда R₂ = 0 и R₁ << w L, резонанс наступит при

.

Резонанса можно достичь путем изменения w, L, С или путем изменения R₁ и R₂. Ток в неразветвленной части схемы по величине может быть меньше, чем токи в ветвях схемы. При R₂ = 0 и R₁ 0 ток I может оказаться ничтожно малым по сравнению с токами I₁ и I₂.

В идеализированном, практически не выполнимом режиме работы, когда R₁ = R₂ = 0, ток в неразветвленной части схемы рис.3.11, а равен нулю и входное сопротивление схемы равно бесконечности. При этом частота, на которой наступает резонанс равна:

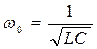. (3.22)

Из (3.21) следует, что частота на которой наступает резонанс в реальной параллельной цепи рис.3.11, а:

. (3.23)

Резонанс в схеме последовательного соединения R, L, С (рис.3.2) называют резонансом напряжений.

При резонансе ток в цепи должен совпадать по фазе с э.д.с. Е. Это возможно, если входное сопротивление схемы (cм. формулу 3.12):

будет чисто активным, т.е. когда выражение в скобках будет равно нулю. Таким образом, условие резонанса в последовательной R, L, С цепи

. (3.24)

Из (3.24) следует, что частота на которой наступает резонанс в последовательной цепи рис.3.2:

. (3.25) Топографическая диаграмма напряжений для режима резонанса показана на рис.3.12.

⇐ Предыдущая 8 9 10 11 12 13 141516 17 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: