Рівняння поверхні еліпсоїда. 2.1. Параметри земного еліпсоїда, зв'язки між ними.

РОЗДІЛ 2

ГЕОМЕТРІЯ ЗЕМНОГО ЕЛІПСОЇДА

2.1. Параметри земного еліпсоїда, зв'язки між ними.

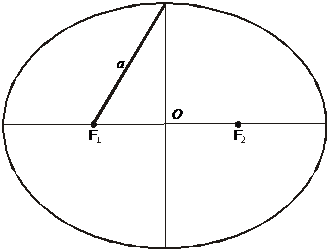
Поверхня еліпсоїда утворюється від обертання еліпса навколо його малої (полярної) осі.

Рис. 2.1

Будь-який еліпс визначається розмірами його великої а і малої b півосей (рис 2.1). За розмірами півосей можна знайти положення фокусів F₁ і F₂ еліпса

Відносна величина, що визначається із співвідношення

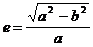(2.1)

називається першим ексцентриситетом еліпса.

Мають застосування і інші відносні величини:

другий ексцентриситет

, (2.2)

полярне сплющення (стиснення)

. (2.3)

Розміри еліпса визначаються розмірами його великої півосі а. Форма еліпса визначається однією із приведених вище відносних величин, найчастіше це сплющення.

Крім великої та малої півосей еліпса, часто застосовується ще одна лінійна величина, що визначається із співвідношення

(2.4)

Приведені лінійні та відносні величини еліпса називаються параметрами еліпса і відносяться також і до еліпсоїда обертання. Параметри а – велика (екваторіальна) піввісь еліпсоїда і b - мала (полярна) піввісь еліпсоїда або a і a називають основними параметрами, що визначають еліпсоїд обертання, а квадрати першого та другого ексцентриситетів е² та - похідними.

Між перерахованими величинами існують залежності. Так із (2.1) та (2.2) отримаємо:

,

,

, (2.5)

.

Враховуючи вище наведені залежності для полярного сплющення a та першого ексцентриситета е отримаємо наступні формули зв'язку

(2.6)

Для виводу числових значень параметрів земного еліпсоїда, переважно великої півосі та сплющення, використовуються відповідні геодезичні, астрономічні, гравіметричні і супутникові виміри.

Для наближених розрахунків можна використовувати наступні значення:

a= 6378 км,

а-b= 21 км,

е²» 2a» .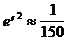

Відомо багато еліпсоїдів, параметри яких визначались в різних регіонах Землі і названі на честь видатних вчених, керівників робіт, що їх визначали:

Таблиця 2.1

Для еліпсоїда Красовського, що застосовується в геодезичних роботах в Україні, крім основних параметрів (див. табл. 2.1), згідно приведених вище формул зв'язку, маємо

b = 6356863.01877;

e² = 0.006693421623;

На даний час, згідно резолюції XVII Генеральної Асамблеї Міжнародної геодезичної та геофізичної спілки (Канбера, 1979), офіційною референцною системою Міжнародної асоціації геодезії є Геодезична Референцна Система 1980 року -GRS80. Ця система визначає основні параметри загального земного (глобального) еліпсоїда. Серед них

a =6378137 м,

a = ,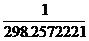

e² = 0.006694380023;

Відзначимо, що прийняття загального земного чи референц-еліпсоїда, тобто його розмірів, є одним з основних чинників, що характеризує певну систему геодезичних координат.

Рівняння поверхні еліпсоїда

Поверхня, як відомо із аналітичної геометрії, визначається рівнянням

F(x,y,z)=0 (2.7)

в прямокутних декартових координатах.

Поверхню можна ще визначити з допомогою трьох рівнянь:

(2.8)

що виражають координати x, y, z у функції довільних параметрів u, v. Виключивши ці парметри із трьох рівнянь (2.8), прийдемо до рівняння виду (2.7). Якщо в рівняннях (2.8) надамо параметрам u, v певні значення, то і для x, y, z отримаємо цілком визначені значення. Отже, кожній парі значень відповідає певна точка на даній поверхні.

Параметри u, відіграють, очевидно, роль координат на даній поверхні; їх називають криволінійними координатами.

Надамо параметру в рівнянні (2.8) яке-небудь постійне значення, а параметр u будемо змінювати. Рівняння (2.8) в такому випадку виражають x, y, z у функції одного довільного параметра u і, відповідно, визначають деяку лінію на поверхні. Змінюючи значення параметра, отримаємо множину ліній .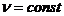

Цілком аналогічно маємо другу множину ліній . Лінії тієї і другої множини називаються координатними лініями; вони аналогічні прямим на площині, що визначаються рівняннями x=const і y=const.

Із аналітичної геометрії відомо, що рівняння поверхні двоосного еліпсоїда обертання може бути записане у вигляді

. (2.9)

Це-рівняння виду (2.7)

Для поверхні еліпсоїда обертання рівняння виду (2.8) матимуть вигляд

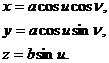(2.10)

Виключення параметрів u, із рівнянь (2.10), як було сказано вище, повинно привести до рівняння (2.9). Із перших двох рівнянь (2.10) отримаємо

.

Це рівняння і третє рівняння (2.10) можуть бути написані в наступному виді

Їхня сума і дає нам рівняння (2.9).

Вияснимо геометричний зміст координатних ліній. Перш за все розглянемо лінію u=const.

Позначимо

(2.11)

тоді

-- рівняння кола (2.12)

Ці формули показують, що площина z=const (рис 2.2) паралельна площині ху і перетинає поверхню еліпсоїда по колу радіуса r.

Рис. 2.2

Коло u=const називається паралеллю, а параметр 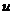– широтою.

Паралель з найбільшим радіусом r=a (z=0) називається екватором. Екватор ділить еліпсоїд на дві симетричні половини.

Криві =const є еліпсами і утворюються в результаті перетину поверхні еліпсоїда площинами, що вміщують вісь z. Вони називаються меридіанами, а параметр , який для поверхні еліпсоїда позначається буквою – геодезичною довготою.

Якщо в рівнянні (2.9) виключити координати за (2.12), то отримаємо рівняння меридіана

(2.13)

Широта 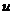та довгота є криволінійними координатами точки на поверхні еліпсоїда; рівняння (2.13) – це рівняння еліпса, параметризоване широтою u, яка носить назву - п р и в е д е н а широта.

Приведена широта 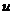може бути побудована геометрично. Візьмемо відрізок прямої, рівний великій півосі еліпсоїда, і відкладемо його так, щоб один кінець відрізка лежав на поверхні еліпсоїда в деякій точці Q, а другий – на осі обертання еліпсоїда в точці Q^’ (рис 2.3)

Гострий кут, утворений відрізком QQ^’ з площиною екватора, називається приведеною широтою.

Поверхня може бути задана також змінним радіусом–вектором r, та геоцентричною широтою .

Геоцентричною широтою називається кут, утворений радіусом–вектором даної точки з площиною екватора.

Рис. 2.3

Із прямокутного трикутника (рис2.3) отримаємо

, (2.14)

або

(2.15)

Із трикутника (рис2.3) для радіуса-вектора отримаємо наступні вирази

(2.16)

а враховуючи (2.13), радіус-вектор еліпсоїда у функції геоцентричної широти буде

(2.17)

Не нашли, что искали? Воспользуйтесь поиском: