Зв'язок між геодезичною, приведеною і геоцентричною широтами.

Для того щоб встановити зв'язок геодезичної широти В з приведеною и, розглянемо який-небудь меридіан, наприклад, такий, площиною якого є площина zx (див. рис.2.2). Для цього меридіана L=const і його рівняння в параметричній формі отримаємо із рівнянь (2.10)

Тангенс кута, утвореного нормаллю з віссю х (рис.2.4), рівний похідній 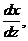взятій з оберненим знаком, тобто

,

або

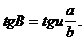
Рис. 2.4

Із останньої формули легко можна отримати

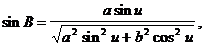
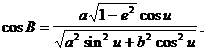
Ввівши позначення

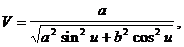
отримаємо наступні формули зв'язку між геодезичною 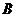та приведеною 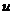широтами

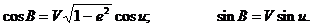(2.18)

Приймаючи до уваги третю формулу (2.5), отримаємо

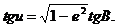(2.19)

На основі формул (2.15) та (2.19) зв'язок між геоцентричною широтою та геодезичною 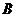буде наступним

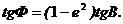(2.20)

Для подальшого викладу нам будуть необхідні ще наступні залежності, що легко отримуються із (2.19)

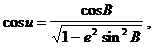
(2.21)

Якщо ввести позначення

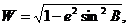(2.22)

то формули (2.21) будуть мати наступний вид

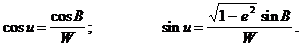(2.23)

Згідно формул (2.23) і (2.18) можна записати зв'язок між величинами V та W

. (2.24)

Із формули (2.24) з врахуванням (2.22) та зв'язку між ексцентриситетами (перша формула із 2.5) отримаємо вираз для V у функції геодезичної широти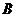

2.25)

Функції V та W називають ще основними сфероїдними функціями геодезичної широти.

У сфероїдній геодезії часто використовується позначення

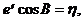(2.26)

тоді

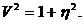(2.27)

Не нашли, что искали? Воспользуйтесь поиском: