ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Обчислення площі сфероїдної трапеції. Для обчислення площі формулу (2.50), з врахуванням (2.67), представимо в наступному вигляді
Для обчислення площі формулу (2.50), з врахуванням (2.67), представимо в наступному вигляді
 (2.68)
(2.68)
після чого використаємо прийом, аналогічний як при знаходженні інтегралу (2.51), а саме, підінтегральну функцію (2.68) розкладемо в біномінальний ряд:
 .
.
Застосовуючи загальну формулу інтегрування
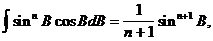
отримаємо
 (2.69)
(2.69)
У формулі (2.69) 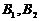 та
та  - геодезичні координати вершин сфероїдної (знімальної) трапеції.
- геодезичні координати вершин сфероїдної (знімальної) трапеції.
Якщо задана номенклатура знімальної трапеції, площу якої необхідно обчислити, то перш за все необхідно визначити геодезичні координати 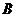 і
і  її вершин. Для цього спочатку з допомогою бланкової номенклатури карти знаходять координати вершин трапеції масштабу 1:1000 000, а потім за стандартною процедурою (методом поділу масштабів) геодезичні координати вершин, заданої певним масштабом, трапеції.
її вершин. Для цього спочатку з допомогою бланкової номенклатури карти знаходять координати вершин трапеції масштабу 1:1000 000, а потім за стандартною процедурою (методом поділу масштабів) геодезичні координати вершин, заданої певним масштабом, трапеції.
Числовий приклад.
Для листа карти  масштабу 1: 1 000 000 В2 =52°, В1 =48°, різниця довгот східної і західної рамок карти
масштабу 1: 1 000 000 В2 =52°, В1 =48°, різниця довгот східної і західної рамок карти  . Тоді, згідно формули (2.69), для еліпсоїда Красовського площа трапеції
. Тоді, згідно формули (2.69), для еліпсоїда Красовського площа трапеції  дорівнює
дорівнює  км2.
км2.
Коли мова йде про дійсну площу ділянок фізичної поверхні Землі, то її підраховують не за приведеними формулами, а шляхом безпосереднього вимірювання площ на топографічних картах чи планах.
Для обчислення площі всієї поверхні земного еліпсоїда у формулі (2.69) треба прийняти 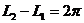 ,
,  . Тоді
. Тоді
 . (2.70)
. (2.70)
На основі цієї формули можна знайти радіус еквівалентної кулі  , площа якої дорівнює площі еліпсоїда
, площа якої дорівнює площі еліпсоїда 

звідки
 (2.71)
(2.71)
Радіус кулі, рівновеликої за площею поверхні загального земного еліпсоїда WGS-84, дорівнює, згідно формули (2.71) 6370894м. Це значить, що при розв'язуванні деяких задач, в основному, наближеного характеру, коли форму Землі можна прийняти за кулю, її радіус потрібно брати 6371км.
Крім площі трапеції, на практиці приходиться обчислювати і лінійні розміри її рамок в масштабі карти. Рамки трапеції - це відрізки дуг меридіанів і паралелей. Формули для довжин рамок трапецій, у відповідності з формулами (2.63) та (2.67), будуть
 , (2.72)
, (2.72)
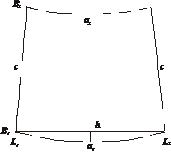
де  - знаменник масштабу карти. Позначення сторін трапеції показані на рис. 2.11.
- знаменник масштабу карти. Позначення сторін трапеції показані на рис. 2.11.
|
Рис. 2.11
Стрілку прогину рамки знімальної трапеції розраховують за формулою
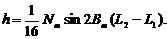 (2.73)
(2.73)
Зазначимо, що всі кутові величини, які входять у вищенаведені формули безпосередньо, треба брати в радіанній мірі.
Не нашли, что искали? Воспользуйтесь поиском: