Основные свойства преобразования Лапласа

Очевидно, что соответствие между оригиналом и изображением взаимно однозначны, т. е. каждой функции f(t) соответствует одна вполне определенная функция F(p) и наоборот.

Свойство линейности. При умножении оригинала на постоянную величину на ту же постоянную величину умножается и изображение

а f(t) а F(p).

Действительно,

.

Если оригинал представлен суммой функций, то изображение этой суммы равно сумме изображений этих функций (свойство линейности преобразования Лапласа: изображение линейной комбинации функций есть линейная комбинация изображений)

.

Теорема дифференцирования. Допустим, что некоторая функция f(t) имеет изображение F(p), требуется найти изображение производной этой функции.

Пусть . Найти .

.

Интегрируя по частям, получим

,

.

Вычисление производной при нулевых начальных условиях [f(0) = 0] соответствует умножению изображения функции на множитель p:

, .

Теорема интегрирования. Известно изображение некоторой функции f(t). Требуется определить изображение функции, являющейся интегралом функции f(t).

Пусть , тогда ,

если = 0 , то ,

f(t) F(p), F(p) = , , .

Многократному интегрированию соответствует общее выражение

.

Теорема запаздывания. Теорема позволяет определить изображение функции , отличающейся от функции f(t) тем, что она сдвинута вправо вдоль оси времени на (рис. 1.49)

Рис. 1.49

,

так как в интервале функция = 0.

Введем новую переменную , тогда , .

.

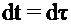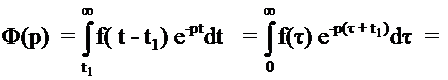
Таким образом, запаздывание функции на время соответствует умножению её изображения на .

Теорема смещения. Теорема смещения позволяет определить, как изменяется изображение при умножении оригинала на показательную функцию , где a - постоянное число.

Пусть новая функция имеет вид .

Изображение

.

Таким образом, умножение временной функции на экспоненциальный множитель приводит к «смещению» в области изображений независимой переменной p на .

Теорему смещения очень удобно применять при определении изображения экспоненциально убывающих функций. Например, необходимо найти изображение функции .

Выше было показано, что , тогда

.

Разделив вещественную и мнимую части, получим

, .

Следовательно,

.

Теорема умножения изображений (теорема свертки - интеграл Бореля)

заключается в следующем: если

, ,

то

Таким образом, произведению изображений двух функций соответствует свертка их оригиналов. Теорема свертки широко используется при составлении таблиц операторных соотношений. Если изображение искомой функции может быть представлено в виде произведения двух (или более) сомножителей, то по оригиналам каждого из сомножителей можно вычислить оригинал исходной функции. Например, определим оригинал функции, изображение которой имеет вид

.

Изображение Ф(р) можно представить как произведение двух изображений:

,

.

Следовательно,

.

Теорема подобия позволяет определить изображение функции времени при изменении масштаба её аргумента. Пусть известно изображение функции f(t) F(p). Определим изображение функции j(t) = f(a t), где а - некоторая положительная постоянная.

.

Обозначим at = x, тогда и

.

Окончательно имеем

f(a t) .

Умножение аргумента оригинала на положительное постоянное число а приводит к делению аргумента изображения и самого изображения на то же число а.

Предельные соотношения устанавливают существование равенства между значениями функции времени и её изображения в начале координат и в бесконечно удаленной точке.

, .

Ниже будет показано, что комплексную переменную р можно рассматривать как обобщенную (комплексную) частоту, мнимая часть которой представляет собой угловую частоту некоторого гармонического колебания, а вещественная характеризует изменение огибающей этого колебания. Приняв вещественную часть р равной нулю, получим из предельных соотношений связь между функцией времени и частотной характеристикой в начале координат и при бесконечных значениях t и jw.

Проиллюстрируем эту связь на примере прохождения импульсного сигнала через усилитель с ограниченной полосой пропускания (рис. 1.50).

Рис. 1.50

Таким образом, характер изменения функции времени в области малых времен определяется частотной характеристикой в области высоких частот и наоборот: изменения в области больших времен определяется частотной характеристикой в области низких частот.

Не нашли, что искали? Воспользуйтесь поиском: