Калорическое и термическое уравнения состояния системы

Уравнение (П.4.1) является универсальным, и, в этой связи, применимым для всех типов макроскопических систем. Однако, даже для простейшего случая термодинамической системы (идеальный газ)

,

(П.4.2)

это уравнение является неразрешимым, поскольку содержит пять переменных 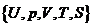. Следовательно, его практическое применение для конкретной термодинамической системы сопряжено с необходимостью дополнения к этому уравнению ряд дополнительных соотношений, характеризующих специфику рассматриваемой системы.

Для изыскания этих соотношений следует обратить внимание на тот факт, что равновесные внутренние параметры системы являются функциями внешних параметров и температуры системы, что приводит к существованию термических и калорических уравнений состояния системы. Эти дополнительные уравнения должны связывать температуру T и внешние параметры a_i с каким либо внутренним параметром b_k термодинамической системы:

(П.4.3)

Если в качестве внутреннего параметра b_k выступает непосредственно внутренняя энергия системы U (т.е.: b_k = U), то получается калорическое уравнение состояния системы:

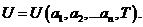
(П.4.4)

Своим названием калорическое уравнение состояния обязано тому обстоятельству, что с его помощью можно находить теплофизические характеристики материалов, например, теплоемкость веществ.

Если же внутренним параметром b_k является сопряженная внешнему параметру a_i обобщенная сила A_i (т.е. b_k = A_i), то получается термическое уравнение состояния системы:

где: i = 1, 2,… n.

(П.4.5)

Своим названием термическое уравнение состояния обязано тому обстоятельству, что с его помощью можно находить температуру системы.

Общее число термических и калорических уравнений состояния системы равно числу ее степеней свободы, т.е. числу независимых параметров однозначно характеризующих состояние системы. Согласно постулатам равновесной термодинамики калорическое и каждое из термических уравнений состояния системы не являются независимыми (связаны дифференциальным уравнением в частных производных).

Если калорическое и все термические уравнения состояния системы известны, то далее, с помощью теоретического аппарата термодинамики, можно определить все термодинамические свойства системы. Важно отметить, что вывести (теоретическим путем) упомянутые выше уравнения состояния системы с помощью методов термодинамики не представляется возможным. Эти уравнения устанавливаются либо опытным путем, либо – с помощью теоретического аппарата статистической физики.

Методологические принципы практического использования калорического и термических уравнений состояния удобно проиллюстрировать на примере анализа простейшей термодинамической системы – «идеальный газ», для которой эти уравнения имеют соответственно вид (обратить внимание на то, что система имеет две степени свободы):

	(термическое уравнение).	(П.4.6.а)
	(калорическое уравнение).	(П.4.6.б)

Если принять в качестве обобщенной силы (давление газа) и сопряженную этой силе обобщенную координату 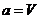(объем газа), то уравнения состояния приобретают вид:

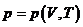	(термическое уравнение).	(П.4.7.а)
	(калорическое уравнение).	(П.4.7.б)

Для идеального газа термическим уравнением состояния является известное уравнение Клайперона-Менделеева (определено эмпирическим путем!):

(термическое уравнение).

(П.4.8)

Обратить внимание на то обстоятельство, что наличие выражения (П.4.8) уменьшает число степеней свободы термодинамической системы на единицу.

Используя закон Джоуля о независимости внутренней энергии идеального газа от его объема при постоянной температуре (т.е. исключается из рассмотрения потенциальная энергия взаимодействия атомов газа между собой: ), для калорического уравнения имеем:

,

(П.4.9)

где - теплоемкость газа при постоянном объеме.

Согласно опытным данным, теплоемкость не зависит от температуры газа (элемент идеализации в постановке задачи), поэтому, в результате интегрирования выражения (П.4.9), для калорического уравнения имеем:

,

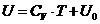(П.4.10)

где - постоянная интегрирования, зависящая только от типа рассматриваемого газа.

Рассмотренный случай («идеальный газ») является самым простым в практике анализа термодинамических систем. Уже для случая «реальных газов» (не говоря уж о конденсированных средах) трудности нахождения уравнений состояния системы неизмеримо возрастают. Именно это обстоятельство является сдерживающим фактором на пути широкого использования (внедрения) теоретических подходов равновесной термодинамики в производственно-техническую практику, связанную с созданием устройств электронной техники.

Не нашли, что искали? Воспользуйтесь поиском: