
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 5..Расчеты с использованием векселей.
В конце 50-ых годов возник новый тип финансово-кредитных операций- а форфэ. Эта операция получила распространение во внешней торговли, где она послужила важным стимулирующим фактором развития. Заметим, что нет никаких веских причин, препятствующих ее применению и во внутристрановой торговле.
К форфейтированию прибегают при продажи какого-либо крупного объекта. Покупатель (импортер) приобретает товар в условиях, когда у него нет соответствующих денежных средств. Вместе с тем, продавец (экспортер) так же не может отложить получение денег на будущее и продать товар в кредит. Противоречие разрешается следующим образом, покупатель выписывает пакет векселей (комплект) на сумму, равную стоимости товара плюс проценты за кредит, который как бы предоставляет продавец покупателю. Обычно предусматриваются равные интервалы времени между платежами по векселю. Продавец сразу же после получения портфеля векселей учитывает его в банке без права оборота сделки. Таким образом, фактически не сам продавец кредитует покупателя- кредит полностью предоставляется банком. Банк, форфетируя сделки, берет весь риск на себя. Итак, в операции а форфэ, увязываются интересы продавца, покупателя и банка. В качестве четвертого агента сделки иногда выступает гарант-банк покупателя, гарантирующий погашение задолженности по векселям. Каждая участвующая в сделке сторона, преследует собственные цели и предусматривает возможность их достижения при разработке условий соглашения.
Цель продавца - получить деньги в начале сделки и тем самым устранить риск отказа покупателя от платежа и риск, связанный с колебанием процентной ставки по кредиту.
Цель покупателя - приобрести продукцию в кредит с наименьшими совокупными издержками. Расходы покупателя заключаются в погашении последовательного предъявленным ему векселей.
Для банка форфейтная операция- обычная операция учета портфеля векселей. Эффективность этой операции определяется размером учетной ставки и рядом других параметров.
Анализ операции афорфэ можно осуществить с позиции каждого из участвующих в нем агентов с учетом указанных выше целей. Следует подчеркнуть, что интересы сторон здесь перемещены в большей мере, чем это может показаться на первый взгляд. В связи с этим, анализируя позицию каждого участника операции, необходимо принимать во внимание интересы остальных ее участников.
Анализ позиции продавца.
Определение сумм векселей. Продавец должен получить при учете векселей сумму, равную цене товара. Соответственно, анализ для него заключается в определении сумм, которые должны быть указаны на векселях. Если окажется, что учет векселей дает величину, меньшую, чем оговоренная цена, то продавец должен заранее поправить положение. Обычно на практике для этого повышают исходную цену. Альтернативой может служить повышение ставки процентов за кредит. Ясно, что какой бы путь ни был принят, повышение исходной цены или ставки процентов не может быть произвольным.
Сумма, проставленная на векселе V, (face value), состоит из двух элементов: суммы, погашающей основной долг (цену товара), и процентов за кредит. Последние могут быть определены двумя способами:
а) проценты на остаток задолженности; в этом случае срок, за который они начисляются, начинается с момента погашения предыдущего векселя;
б) проценты на ту часть долга, которая покрывается векселем; в этом случае срок исчисляется от начала сделки и до момента погашения векселя.
Рассмотрим оба способа для случая, когда долг погашается равными суммами. Введем обозначения:
n — число векселей или периодов;
i — ставка простых процентов за период, под которую производится кредитование;
d — простая учетная ставка, используемая банком при учете векселей;
Р — цена товара (если условия операции предусматривают выплату аванса, то последний вычитается из цены и далее не принимается во внимание; иначе говоря, под Р будем понимать цену за вычетом аванса).
Вариант а. Погашение основного долга производится равными суммами, соответственно в каждый вексель записывается сумма Р/n. Что касается процентов за кредит, то они образуют ряд:

Сумма векселя, погашаемого в момент t/

Общая сумма начисленных процентов равна
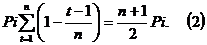
Наконец, общая сумма векселей составит

Вариант б. В этом случае по определению
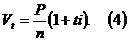
Сумму процентов за весь срок можно найти как разность:
 (5)
(5)
Получен тот же результат, что и по формуле (2). Различие между вариантами, как показано в примере 1, заключается в распределении процентов по периодам.
ПРИМЕР 1. В уплату за товар Р = 1 млн. руб. выписано четыре векселя с погашением по полугодиям. Ставка процентов за кредит — 10% годовых (простых). Таким образом, i = 5%, n = 4, Р: n = 1000: 4 = 250 тыс.руб.
Определим процентные платежи и суммы векселей двумя методами (все показатели в тыс. руб.).
Таблица 1
| T | Pin | Вариант а | Вариант б | ||
| % | Vt | % | Vt | ||
| Итого | - | 50,0 7,5 25,0 12,5 | 300,0 287,5 275,0 262,5 | 12,5 25,0 37,5 50,0 | 262,5 275,0 287,5 300,0 |
Как видим, сумма процентов в обоих вариантах расчета одинакова. Однако распределение платежей во времени противоположное: в варианте а они уменьшаются, в варианте б — растут.
Для покупателя вариант б на первый взгляд представляется более привлекательным.
Корректировка условий продажи. При учете портфеля векселей в банке продавец получит некоторую сумму А. Если применяется простая учетная ставка, как это обычно и делается, то

Величина А представляет собой современную величину всех платежей по векселям. Поскольку сумма на векселе определяется двумя способами, найдем величину А для каждого из них.
Вариант а. В этом случае

После ряда преобразований (7) (см. Математическое приложение к главе) получим

Обозначим сумму в квадратных скобках через z. Очевидно, что если величина z меньше 1, то продавец получит сумму, которая меньше договорной цены Р. Наиболее простой путь избежать потерь — повысить цену в 1/z раз. Такой корректировочный множитель позволяет точно определить необходимую поправку и, кроме того, дает возможность проследить влияние всех воздействующих факторов. В редком случае, когда z = 1 и нет необходимости в корректировке, продавец получает при
учете векселей оговоренную сумму.
Не надо забывать, что после корректировки цены необходимо вернуться к задаче определения сумм векселей уже для новой цены товара.
ПРИМЕР 2. По данным примера 14.1 в случае, когда учетная ставка 9,5% годовых, получим следующее значение коэффициента z:

Таким образом, если все условия сделки останутся без изменений, то продавец получит несколько меньшую вместо оговоренного 1 млн. руб. Повышение цены на
1/z=1/0.994375=1.005657
компенсирует потерю продавца. Суммы векселей после корректировки составят 301,697; 289,126; 276,566; 263,984. Учет этих векселей по ставке 4,75% за полугодие дает в сумме точно 1 млн. руб.
Вероятно, представляет практический интерес соотношение процентных ставок, при которых продавец не будет нести потери. Из равенства (8) следует, что последнее условие выполнимо в случае, когда

В силу чего барьерная процентная ставка, при которой отпадет необходимость в корректировке цены, составит

Повышение платы за кредит до уровня i* полностью балансирует условия сделки. Разумеется, что суммы векселей при этом несколько повысятся.
ПРИМЕР 3. Каков должен быть уровень процентной ставки за кредит для того, чтобы покупатель не понес ущерба в операции а форфэ при условии, что d = 4,75% (данные примера 1, вариант а расчета сумм векселей). В этом случае
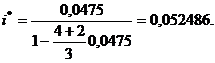
Таким образом, повышение годовой ставки кредита до 10,4972% полностью компенсирует потерю продавца. Альтернативой может служить повышение цены товара (см. пример 2).
Вариант б. Напомним, что по этому варианту проценты начисляются на ту часть долга, которая погашается векселем. По определению

После ряда преобразований этого выражения получим
 (9)
(9)
Корректирующий цену множитель равен 1 / z.
ПРИМЕР 4. Определим корректирующий множитель к цене по данным примера 1 (вариант б) при условии, что d = 4,75%. В этом случае согласно формуле (9)

Корректирующий множитель равен 1/0,988437 = 1,0116977. Как видим, нужна более существенная корректировка цены, чем по варианту а.
Перейдем теперь к корректировке условий сделки с помощью изменения ставки процента за кредит. Единственное значение i, при котором продавец не терпит убытки в варианте б, нетрудно определить из условия, согласно которому t = 1. Для того чтобы удовлетворить это требование, необходимо выполнение условия, которое следует из (9):

откуда
 (10)
(10)
ПРИМЕР 5. По данным примера 1 (вариант б) и при условии, что d = 4,75%, находим

Таким образом, у покупателя имеются две возможности для компенсации потерь при учете портфеля векселей — повысить цену товара на 1,0116977 или увеличить ставку за кредит до
11,0787% годовых.
Корректировка цены и ставки по кредиту приводит примерно к одинаковым конечным результатам, однако обычно наблюдается небольшое различие в суммах векселей. Для иллюстрации сказанного обратимся к примеру.
ПРИМЕР 6. Первоначальные условия сделки: Р = 1200 тыс.руб., ставка по кредиту за полугодие — 3%, учетная ставка за полугодие — 4,5%. Проценты начисляются на сумму векселя (вариант б). Выписывается шесть векселей с последовательным погашением по полугодиям. Поскольку;' < d, то сразу можно сказать, что необходима корректировка исходных условий. Корректирующий множитель, рассчитанный по формуле (9), составит 1,07872. Таким образом, сумма векселя с поправкой, но без начисленных процентов равна 200 х 1,07872 = 215,74. Суммы векселей с начисленными процентами по ставке 3% показаны в табл. 2.
Применив второй метод корректировки, находим

Значения сумм векселей, полученных наращиванием 200 тыс.руб. по ставке 5,59%, приведены в табл. 2.
| Период | Умножение на 1/z | Повышение ставки до i* | ||
| Сумма платежа | Дисконт | Сумма платежа | Дисконт | |
| Итого | 222,22 228,69 235,16 241,63 248,11 254,58 1430,39 | 10,00 20,58 31,75 43,49 55,82 68,74 230,38 | 211,18 222,36 233,54 244,72 255,90 267,08 1434,78 | 9,50 20,01 31,53 44,05 57,58 72,11 234,78 |
Нетрудно убедиться в том, что при любом методе корректировки продавец получит сумму, равную оговоренной цене (1200), как это и требовалось доказать. Небольшое различие между итоговыми суммами векселей (и дисконта) объясняется тем, что распределение платежей по срокам несколько различается. В первом случае оно более равномерно (минимальная сумма — 222,22, максимальная — 254,58), во втором — первый вексель выписывается на сумму 211,18, последний — на 267,08. Указанный небольшой сдвиг приводит к увеличению общей суммы платежа по векселям, а также суммы дисконта.
Анализ позиций покупателя и банка
Совокупные издержки покупателя. Последовательность погашения векселей можно рассматривать как поток платежей. Совокупные издержки покупателя с учетом фактора времени равны современной стоимости этого потока. В § 14.2 было показано, что сумма векселя может быть получена двумя путями. Напомним: вариант а — проценты по кредиту начисляются на остаточную сумму долга, вариант б — проценты начисляются на сумму погашения основного долга по векселю. Определим совокупные издержки покупателя для этих двух вариантов с учетом того, что условия сделки сбалансированы, т.е. с необходимой корректировкой цены.
Вариант а. Для этого варианта современная величина платежей по векселям (приведенные совокупные издержки покупателя) составит
 (11)
(11)
где v — дисконтный множитель по рыночной процентной ставке q.
ПРИМЕР 7. По данным примера 1 (вариант а) при условии, что сложная ставка, которая характеризует средний уровень ссудного процента на рынке, равна, допустим, 15% годовых, что соответствует ставке за полугодие q = '\,'\У12 — 1 = 0,07238, или 7,238%. Величины V^ приведены в табл. 1; значение z = 0,994375 найдено в примере 2. Получим:

Вариант б. При начислении процентов на остаток задолженности получим следующее значение современной стоимости потока платежей:

ПРИМЕР 8. Для варианта б начисления процентов (данные примера 2) при условии, что z = 0,988437 (см. пример 4) и q = 7,238%, находим:

Как видим, такой способ начисления процентов при условии, что q > i, Дает сумму совокупных издержек, которая чуть меньше, чем у варианта а.
Минимизация издержек. Современная стоимость издержек покупателя зависит от всех параметров операции, причем при q > i всегда наблюдается соотношение Wg < Wa*. Иначе говоря,
совокупные издержки покупателя меньше при начислении процентов по варианту б. Причем, чем больше т и q, тем больше разность современных стоимостей потоков платежей, соответствующих двум вариантам начисления процентов.
В табл. 3 иллюстрируется влияние роста учетной ставки на приведенные издержки покупателя (вариант 1). Влияние процентной ставки i на величину приведенных издержек неоднозначно. В некоторых случаях ее рост приводит к увеличению W, в других — к уменьшению. Однако в любом случае это влияние мало ощутимо. Оно становится заметным лишь при больших значениях п. В этой же таблице приводятся данные, характеризующие Wб для разных значений i (варианты 2 и 3). При
расчете совокупных издержек приняты следующие параметры: Р = 1000, q = 0,1. В варианте 1 n = 10, i = 0,06; в варианте 2 n = 10, d = 0,07; в варианте 3 n = 8, d = 0,05.
Наиболее интересной и практически важной является зависимость современной стоимости издержек от количества последовательно погашенных векселей n. Нетрудно обнаружить, что при одних сочетаниях исходных параметров операции (i, d, q) значение. Сможет расти, при других — падать. Более того, при некоторых сочетаниях параметров существует такое количество векселей, при котором совокупные издержки покупателя становятся минимальными. Строгий аналитический подход для определения оптимального п приводит к громоздким математическим выражениям. Проще рассчитать ряды показателей для заданного набора параметров и выбрать оптимальное значение n.
Таблица 3.
Не нашли, что искали? Воспользуйтесь поиском: