Школьный этап Всероссийской олимпиады школьников. 1. Поставьте знаки модуля так, чтобы равенство 1 – 2 - 4 – 8 – 16 = 19 стало верным.

По математике

Класс

Задания.

1. Поставьте знаки модуля так, чтобы равенство 1 – 2 - 4 – 8 – 16 = 19 стало верным.

2. Одну овцу лев съедает за 2 дня, волк – за 3 дня, а собака – за 6 дней. За сколько дней они вместе съедят овцу?

3. Число a таково, что прямые y = ax + 1, y = x + a и y = 3 различны и пересекаются в одной точке. Каким может быть a?

4. В треугольнике ABC проведена медиана AD. Найдите углы треугольника ABC, если ADC = 120º, DAB = 60º.

5. На смотре войска Острова лжецов и рыцарей (лжецы всегда лгут, рыцари всегда говорят правду) вождь построил всех воинов в шеренгу. Каждый из воинов, стоящих в шеренге, сказал: «Мои соседи по шеренге – лжецы». (Воины, стоящие в концах шеренги, сказали: «Мой сосед по шеренге – лжец».) Какое наибольшее число рыцарей могло оказаться в шеренге, если на смотр вышли 2005 воинов?

Ответы, указания, решения.

(может быть предложено другое решение)

1. Ответ. || 1 - 2| - |4 - 8| - 16| = 19.

2. Ответ. За один день.

Решение. Лев съедает за день овцы, волк - овцы, собака - овцы. Тогда вместе за день они съедят + + = 1 овца.

3. Ответ. a = 2.

Первое решение. Заметим, что при x = 1 выполняется ax + 1 = x + a = a + 1, так что точка M (1; a + 1) является общей для прямых y = ax + 1 и y = x + a. Так как прямые различны, M – их единственная общая точка. Поэтому прямая y = 3 тоже должна проходить через неё, откуда a + 1 = 3 и a = 2. Легко видеть, что при a = 2 все три прямые действительно различны.

Второе решение. По условию в точке пересечения a x + 1 = x + a, тогда (a – 1)(x – 1) = 0. Значит a = 1 или x = 1. Но случай a = 1 невозможен, потому что тогда первые две прямые совпадали бы. Дальше рассуждаем как в первом решении.

4. Ответ. 90º, 60º, 30º.

Решение. 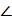ADB = 180º – 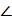ADC = 60º. Тогда 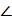ABD = 60º. Значит, треугольник ABD – равносторонний. Откуда AD = BD = DC. То есть треугольник ADC – равнобедренный. Значит, 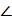DAC = 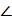DCA = 30º. Следовательно, 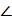BAC = 90º.

5. Ответ. 1003.

Решение. Заметим, что два воина, стоящие рядом, не могли оказаться рыцарями. Действительно, если бы они оба были рыцарями, то они оба сказали бы неправду. Выберем воина, стоящего слева, и разобьем ряд из оставшихся 2004 воинов на 1002 группы по два рядом стоящих воина. В каждой такой группе не более одного рыцаря, т. е. среди рассматриваемых 2004 воинов не более 1002 рыцарей, т. е. всего в шеренге не более 1002 + 1 = 1003 рыцарей.

Рассмотрим шеренгу РЛРЛР...РЛРЛР. В такой шеренге стоит ровно 1003 рыцаря.

Не нашли, что искали? Воспользуйтесь поиском: