Школьный этап Всероссийской олимпиады школьников по математике

Класс

Задания.

1. Постройте график функции

у = .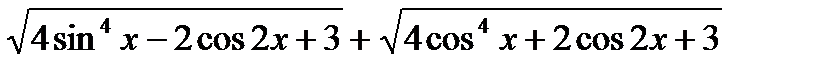

2. Определите а так, чтобы сумма квадратов корней уравнения

х² + (2 – а) х – а – 3 = 0 была наименьшей.

3. Числа x, y, z и t таковы, что x > y³, y > z³, z > t³, t > x³. Докажите, что xyzt > 0.

4. Может ли сумма 100 последовательных натуральных чисел оканчиваться той же цифрой, что и сумма следующих 98 чисел?

5. Четырёхугольник ABCD вписан в окружность. На продолжении диагонали BD за точку D выбрана точка F такая, что AF BC. Докажите, что окружность, описанная около треугольника ADF, касается прямой AC.

Ответы, указания, решения.

(может быть предложено другое решение)

1. Решение. у = ,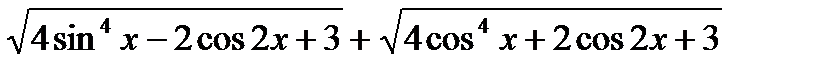

у = ,

у = = 2 sin²x + 1 + 2 cos²x + 1 = 4.

Поэтому графиком функции будет прямая, заданная уравнением у = 4.

2. Ответ. a = 1.

Решение. Найдём сумму квадратов корней уравнения: x₁² + x₂² =

(x₁ + x₂)² – 2x₁x₂ = (2 – a)² + 2(a + 3) = a² – 4a + 4 + 2a + 6 =

a² – 2a + 10 = (a – 1)² + 9. Значение данного выражения будет наименьшим при a = 1. При этом значении a дискриминант левой части уравнения положителен, поэтому корни существуют.

3. Решение. Пусть x < 0, тогда из первого неравенства следует, что y³ < 0, то есть y < 0.Далее аналогично z < 0 и t < 0. Значит, все четыре числа отрицательны, и их произведение положительно.

Если x > 0, то из последнего неравенства t > 0, и далее аналогично z > 0 и y > 0, откуда xyzt > 0.

Если же x = 0, то тогда из первого неравенства следует, что y³ < 0, то есть y < 0. Далее аналогично z < 0 и t < 0. После этого из последнего неравенства следует, что x < 0;противоречие. Итак, случай x = 0 невозможен.

4. Ответ. Не может.

Первое решение. Заметим, что сумма 100 последовательных натуральных чисел является чётным числом, так как содержит ровно 50 нечётных слагаемых. А сумма 98 последовательных натуральных чисел является нечётным числом, так как содержит ровно 49 нечетных слагаемых. Поэтому эти суммы оканчиваются на цифры разной чётности.

Второе решение. Заметим, что сумма 100 последовательных натуральных чисел оканчивается на 0, а сумма никаких двух подряд идущих чисел на 0 не оканчивается. Значит, не заканчивается на 0 и сумма никаких 98 подряд идущих чисел.

5. Решение. Условие касания равносильно тому, что угол CAD между прямой CA и хордой AD равен половине градусной меры дуги AD, то есть вписанному углу AFD, опирающемуся на эту дугу.

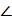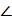Но из параллельности прямых BC и AF следует, что AFD= DBC = 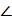CAD (последнее равенство вытекает из того, что вписанные углы DBC и CAD опираются на одну дугу CD), что и требовалось.

Не нашли, что искали? Воспользуйтесь поиском: