Кристаллический потенциал и свойства симметрии гамильтониана

Уравнения Хартри – Фока (4.2) справедливы для любой многоэлектронной системы с произвольным числом ядер, в том числе, и для твёрдого тела. Перепишем теперь это уравнение в другом виде, более удобном для анализа:

, (5.1)

где H –функция Гамильтона имеет вид

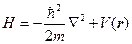. (5.2)

Здесь – потенциальная энергия электрона. Из всего, изложенного выше, следует, что для такой системы как твёрдое тело она состоит из кулоновской потенциальной энергии электронов в поле всех ядер (второе слагаемое в (4.2)); кулоновской же потенциальной энергии взаимодействия электронов друг с другом (третье слагаемое в(4.2)); и, наконец, четвёртое слагаемое в(4.2) – потенциальная энергия обменного взаимодействия. Таким образом, для потенциальной энергии электрона в твёрдом теле, и которую в дальнейшем будем называть кристаллическим потенциалом, можно записать такое выражение

. (5.3)

Остановимся коротко на свойствах симметрии гамильтониана. Так как каждое твёрдое тело имеет свою пространственную группу симметрии, состоящую из всевозможных вращений и подгруппы трансляции, то, для выяснения этих свойств, очевидно, нужно рассмотреть поведение функции (5.2) под действием операций группы. Прежде всего, ясно, что первое слагаемое, являющееся скалярным дифференциальным оператором, является инвариантом относительно любых вращений и трансляций. Второе слагаемое – потенциальная энергия также являющаяся скалярной функций инвариантна относительно всех преобразований группы. Следовательно, можно сделать заключение – функция Гамильтона электрона в кристалле обладает всеми свойствами симметрии пространственной группы кристалла. Отсюда следует вывод, что решение уравнение (4.8) – уравнения Шрёдингера можно искать только внутри элементарной ячейки кристалла.

Широко распространенным кристаллическим потенциалом является так называемый потенциал в МТ («маффин–тин») или ячеечное приближение. Суть этого приближения заключается в следующем. Весь кристалл разбивается на области двух типов. Для каждого из них принимают свй вид потенциала. Это обусловлено тем, что кристаллический потенциал V(r), как и атомный, быстро меняется лишь вблизи ядра. Каждый атом кристалла окружается МТ – сферой. Внутри сфер потенциал выбирают в виде сферически симметричной функции V (| r |), а вне сфер, заменяют определённым образом выбранной константой :

и если .

Значения радиуса МТ – сфер в некотром смысле произвольно. Обычно это максимально большие неперекрывающиеся сферы, что приводит к уменьшению объёма между сферами и улучшает сходимость используемого метода. Кроме того, данное приближение позволяет искать волновые функции решения уравнения Шрёдингера в виде разложения по сферическим гармоникам.

Теорема Блоха

Поскольку уравнение Шрёдингера является уравнением в частных производных для его решения необходимо установить класс функций и граничные условия для них, которые будут удовлетворять этому уравнению. Задача эта решается учётом симметрии решётки. Поскольку она периодична, распределение зарядовой плотности в каждой ячейке кристалла должно быть одинаковым, а сама ячейка электрически нейтральной. Пусть – волновая функция, описывающая распределение электронов в ячейке, тогда плотность распределения электронов в ячейке, определится соотношением 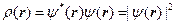. Так как это распределение должно быть периодическим, с периодом решётки кристалла , то мы должны иметь следующее равенство

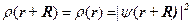. (6.1)

Отсюда можно сделать вывод, что при переходе в ячейку с вектором , волновая функция умножается на некоторое комплексное число , которое можно подчинить условию , т.е. .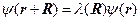

Теперь нетрудно получить, выполнив несколько трансляций на разные вектора решётки, следующие соотношения

.

Отсюда немедленно следует, что . Этому условию и условию можно удовлетворить, если положить , где вектор имеет размерность обратной длины. Таким образом, набор функций, среди которых следует искать решения уравнения Шрёдингера должен удовлетворять следующему условию

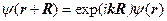.(6.2а)

Это условие и составляет содержание теоремы Блоха. Второе условие, которому должно удовлетворять решение дифференциального уравнение второго порядка, требует непрерывности функции при переходе через границу ячейки, т.е. должна быть непрерывной нормальная производная в двух точках и 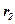на границах, связанных соотношением . Нормали к границам удовлетворяют условию . Это условие имеет вид

. (6.2б)

Условия (6.2а) и (6.2б) называются блоховскими условиями. Таким образом, если обратиться к теории неприводимых представлений полгруппы трансляций, то можно говорить, что решения уравнения Шрёдингера для кристалла являются собственными функциями оператора трансляций 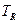. Вектор , нумерующий эти неприводимые представления, в дальнейшем будем называть волновым вектором и писать в качестве индекса у волновой функции .

Не нашли, что искали? Воспользуйтесь поиском: