Приближение свободных электронов

Одноэлектронное уравнене всё ешё является сложным; о его точном решении не мо может идти речи. Поэтому для получения хоть какой–то информации необходимо делать новые приближения. Простейшее из них состоит в пренебрежении в уравнении всеми членами, кроме кинетической энергии. Это так называемая модель свободных электронов Зоммерфельда. Для подробного рассмотрения этой модели сволновой функцией поступим следующим образом. Именно, представим её в таком виде

, (8.1)

где – теперь просто периодическая функция с периодом решётки, т.е.

. (8.2)

Вспоминая теперь, что волновые вектора нумеруют неприводимые представдения подгруппы трансляций (см. §3 гл.2.), мы должны каждую функцию записыватьс волновым вектором . Положим теперь периодическую часть волновой функции (8.1) равной константе, тогда нормированная в объёме кристалла волновая функция может быть записана в виде

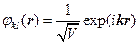. (8.3)

Фактически это приближение соответствует континуальной модели кристалла. Волновой вектор здесь меняется без ограничений на границе зоны Бриллюэна. Если отказаться от этого ограничения, то волновую функцию можно записывать в таком виде

. (8.4)

где – вектор обратной решётки, волновой вектор теперь изменяется только в первой зоне Бриллюэна. Энергия электрона тогда в этом приближении приобретёт вид

. (8.5)

Индекс p здесь имеет смысл номера энергетической зоны, что справедливо только в данном приближении. Выражение (8.5) называют законом дисперсии.

Принятая аппроксимация позволяет рассматривать систему как газ свободных электронов. Частица с номером l обладает квазиимпульсом в первой зоне Бриллюэна , и выражение (8.3) представляет собой квантовомеханическую формулу для волновой функции свободной частицы. Ограничения, налагаемые на волновой вектор , при больших объёмах несущественны и физического значения не имеют. Здесь шёл разговор о квазимпульсе по той причине, чтоволновые функции вида (8.1), как легко проверить, не являются собственнми фунуциями оператора импульса, имеющего вид .

Так как – трёхмерный вектор, полное изображение зонной структуры кристалла потребовало бы использование четырёхмерного пространства. Чтобы преодолеть это затруднение, используют два способа. Можно выбрать какие – то выделенные направления в обратном пространстве и для каждого из этих направлений нарисовать кривые вдоль выбранного направления. Кроме того, можно нарисовать поверхности постоянной энергии, определяемые уравнением

,

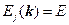Для различных зон j и различных значений постоянной энергии E; каждой из этих поверхностей необходимо приписать определённые значения j и E. Фактически оба эти способа совместимы, если поверхности постоянной энергии рассечь какой – либо плоскостью. Для иллюстрации этого рассмотрим зоны свободных злектронов для простой кубической решётки. В этом случае обратной решёткой так же будет простая кбическая с постоянной решётки , где a – постоянная прямой решётки. В обратной решётке систему координат направим вдоль рёбер куба. Для упрощения записи положим

,

Тогда энергия имеет вид , где целые числа определяют вектор обратной решётки 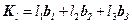. На рис.

представлены энергетические зоны гранецентрированной кубической решётки вдоль оси X [100] и вдоль главной диагонали [111].Эти напрвления обычно одозначают сиволом и . Обозначения кривых и точек на рис. связаны со свойствами симметрии данных направлений. Подобную структуру имеют и энергетические зоны в этом приближении и для других кристаллических структур. Легко видеть, что на границах зоны Бриллюэна наблюдается вырождение энергетических уровней, которое называют случайным.

При рассмотрении неприводимых представлений подгруппы трансляций было показано, что число различных неприводимых представлений, т.е. число различных волновых векторов внутри зоны Бриллюэна равно числу N элементарныз ячеек в кристалле. Однако, поскольку в каждом состоянии могут находиться два электрона, у одного из которых спиновый момент равен 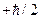, а другого , число разрешённых состояний на одну энергетическую зону внутри зоны Бриллюэна должно быть равно 2 N, т. е. удвоенному числу элементарных ячеек в кристалле. Если полное число электронов проводимости, отдаваемых всеми атомами, находящимися в каждой элементарной ячейке кристалла, равно x, то полное число электронов проводимости, которые нужно разместить в различных возможных состояниях, характеризуемых величинами и , равно xN. Следовательно, эти электроны заполнят xN/2N=x/2 зон в зоне Бриллюэна. Таким образом, при увеличениии размеров кристалла соответственно увеличивается число разрешённых состояний, приходящихся на одну зону, но в равной мере увеличивается и число электронов проводимости, размещаемых в этих состояниях, так что для любой данной зоны занятая доля объёма зоны Бриллюэна не зависит от объёма кристалла.

Какие из 2 N состояний, имеющихся в любой зоне кристалла, будут на самом деле заняты, определяет распределение Феррми–Дирака. Вероятность того, что состояние с волновым вектором в зоне при температуре T будет занято, определяется выражением

, (8.6)

где – энергия Ферми, а k – постоянная Больцмана. Так как волновой вектор можно считать непрерывной переменной, но тогда и будет непрерывной функцией этого вектора. При температурах T близких к абсолютному нулю, все те части зоны , для которых < , будут заняты, а те части, для которых > – свободны. Таким образом, можно говорить, что энергия отделяет при абсолютном нуле температур занятые состояния от свободных. Если рассмотрение вести в терминах поверхностей постоянной энергии, то выделенную поверхность постоянной энергии, соответствующую уравнению

= , (8.7)

можно рассматривать как поверхность, отмечающую границу между занятыми и свободными частями зоны j. Это утверждение остаётся справедливым и при температурах отличных от абсолютного нуля температур, так как обычно реализуется случай . Поверхность постоянной энергии, определяемую уравнением (8.7), называют поверхностью Ферми. Важность этого пнятия мы обсудем позднее.

Не нашли, что искали? Воспользуйтесь поиском: