Химический потенциал и физическая статистика

Любое твёрдое тело представляет собой систему или коллектив, состоящий из огромного числа микрочастиц. В таких системах проявляются специфические, так называемые статистические закономерности, изучаемые статистической физикой. Кроме этого, большие коллективы изучаются также и методами термодинамики, к которым следует отнести такой, например, метод термодинамических потенциалов. Одним из важнейших термодинамических потенциалов является энергия системы E. Для систем с переменным числом частиц N полный дифференциал энергии (первое начало термодинамики) записывается в виде

.

где посредством обозначена частная производная

.

Величина называется химическим потенциалом тела. В термодинамике показывается, химический потенциал тела (состоящего из одинаковых частиц) есть не что иное, как его термодинамический потенциал , отнесённый к одной молекуле . С другой стороны, основываясь на первом начале термодинамики, можно сказать, что химический потенциал выражает изменение энергии изолированной системы постоянного объёма, вызванное изменением в ней числа частиц на единицу.

Рассмотрим условие равновесия системы, полное число частиц которой остаётся неизменным, но частицы могут переходить из одного тела системы в другое. Примером такой системы могут быть два металлических проводника, приведённые в контакт поддерживаемые при постоянной температуре. Пусть химический потенциал электронного газа в первом металле будет , а во втором . Пусть из первого металла во второй перетекает электронов. Это вызовет уменьшение энергии первого металла на и увеличение

энергии второго металла на величину . Для того чтобы металлы находились в равновесии, необходимо, выполнение равенств

, или, .

Отсюда находим условие равновесия: . Это условие равновесия справедливо для контакта любых фаз: твёрдой и жидкой, жидкой и газообразной и т. д.

Рассмотрим статистический способ описания коллектива. Основной особенностью статистического описания закономерностей поведения большого коллектива является их вероятностный характер. Они позволяют предсказать лишь вероятность наступления того или иного события.

По характеру поведения в коллективе все частицы можно разделить на две группы: фермионы и бозоны. К фермионам относятся частицы с полуцелым спином: электроны, протоны, нейтроны и др. К бозонам относятся частицы с целым спином. В коллективе фермионы проявляют ярко выраженное стремление быть «уединенными», что отражается известным принципом Паули: если данное квантовое состояние уже занято фермионом, то никакой другой фермион данного типа не может находиться в этом же состоянии. Бозоны, напротив, могут неограниченно заселять одно и тоже состояние. Поэтому характер поведения коллективов фермионов и бозонов определяется как числом частиц, так и количеством состояний, которые могут заполнять оба типа частиц. Так, например, если выполняется такое соотношение , где N -число частиц, а G - число состояний, то в распоряжении каждой частицы имеется множество свободных состояний и вопроса о заселении одного и того же состояния несколькими частицами не возникает. Поэтому свойства коллектива, как целого не будут зависеть от специфики микро частиц, из которых он состоит. Подобные коллективы называются невырождеными. Если же имеет место соотношение , то вопрос о том, как заселять состояния, поодиночке или коллективно, становится актуальным. В этом случае специфика микрочастиц проявляется в полной мере, оказывая значительное влияние на свойства коллектива, как целого, Такие коллективы называются вырожденными. Такие коллективы, очевидно, могут образовываться только из квантовомеханических объектов, так как только у таких объектов параметры состояния изменяются дискретно, вследствие чего число состояний может быть конечным. У классических объектов параметры состояния меняются непрерывно, поэтому у них число состояний бесконечно большое и поэтому они могут образовывать только невырожденные коллективы. Однако следует заметить, что невырожденные коллективы могут образовывать и квантовомеханические объекты, если .

В связи с таким разделением микрочастиц на вырожденные и невырожденные коллективы для описания их свойств используются и разные физические статистики. Статистика, изучающая невырожденные коллективы, называется классической статистикой Максвелла-Больцмана. Физические статистики, изучающие вырожденные коллективы, называются квантовыми статистиками. Это статистика Ферми- Дирака для фермионов и статистка Бозе-Эйнштейна для бозонов. Из сказанного выше ясно, что в квантовых статистиках фигурируют только квантовые объекты, тогда как в классической статистике могут фигурировать и классические, и квантовые объекты. Если уменьшать число частиц в коллективе или увеличивать число возможных состояний, то вырожденный коллектив станет невырожденным.

В предыдущем параграфе (8) для распределения плотности состояний по энергии в интервале от энергии 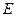до энергии 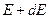было получено такое выражение (с учётом спина электрона)

.(14.1)

На основании этого выражения можно установить критерий невырождености идеального газа. Действительно, проинтегрируем его по энергии от 0 до E, тем самым получим число состояний G для микрочастиц в этом интервале

. (14.2)

Для идеального газа , тогда . После введения концентрации частиц , для критерия невырожденности получим такое выражение

. (14.3)

Рассмотрим это условие для определённого молекулярного газа. Например, для азота при нормальных условиях. В этом случае . Подстановка этих данных в левую часть последнего выражения даёт величину , что значительно меньше единицы. Поэтому обычные молекулярные газы при нормальных условиях являются невырожденными и должны описываться статистикой Максвелла-Больцмана. Применение точно таких же оценок к электронному газу в металлах, для которого , получим, что электронный газ будет невырожденным, лишь при температурах выше . Поэтому в реальных условиях электронный газ в металлах всегда вырожден и должен описываться квантовой статистикой. Однако простейший анализ последней формулы показывает, что невырожденное состояние газа может быть достигнуто не только повышением температуры, но и уменьшением его концентрации. Так, при концентраци , левая часть этого выражения оказывается равной, и электронный газ становится невырожденным. Такая и меньшая концентрация электронного газа может иметь место в полупроводниках, вследствие чего он становится невырожденным и должен описываться классической статистикой.

Согласно (14.3), газ является невырожденным, если средняя плотность заполнения состояний частицами значительно меньше единицы. Так как функция распределения Ферми – Дирака как раз и выражает среднюю плотность заполнения состояний частицами, то условие невырожденности можно записать так

. (14.4)

Это условие будет выполняться, если в (8.6) слагаемое , стоящее в знаменателе, окажется значительно больше единицы, т.е. . Это неравенство должно выполняться для всех состояний, в том числе и для состояния с E=0;

(14.5)

Отсюда следует, что для невырожденности электронного газа, должна быть величиной положительной и существенно большей :

. (14.6)

Сам же химический потенциал должен быть отрицательным и по абсолютной величине большей . Теперь запишем функцию распределения невырожденного газа

Не нашли, что искали? Воспользуйтесь поиском: