Нормальные колебания в трёхмерных кристаллах

Несмотря на простоту одномерных случаев колебанй решётки, они обладают достаточной общностью, что позволило нам выяснить ряд важных свойств волн в решётке, а именно, получить дисперсионные соотношения и доказать существование акустической и оптической ветвей спектра, в дальнейшем на примере этх колебаний мы получим распределения спектра по частотам и найдём плотность состояний. По сравнению с линейной решёткой при рассмотрении двумерных, и трёхмерных кристаллов возникает одна дополнительная характеристика, играющая важную роль. Речь идёт о поляризации волн в решётке.

Основная трудность при изучении динамики решётки в трёхмерном кристалле с одним или несколькими атомами в элементарной ячейке связана с тензорной природой межатомных сил. В результате решения этой задачи дисперсионные кривые теперь становятся зависимыми ещё от одного индекса , где 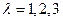определяет поляризацию волны, которые, как известно, в упругой среде подразделяются на продольные и поперечные волны. Поляризация определяется единичным вектором. В общем случае решётки с базисом из r атомов в элементарной ячейке получаются 3 r дисперсионных соотношений 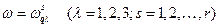. Три нижние ветви дисперсионных кривых, которые приближаются к нулю в пределе длинных волн 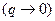, называются акустическими ветвями. В этом случае говорят о продольной волне, если вектор поляризации параллелен волновому вектору q, и о поперечной волне, если вектор поляризации перпендикулярен вектору q. Остальные (3r-3) ветвей являются оптическими; среди них так же различают ветви продольных и поперечных колебаний. На рис. представлены типичные кривые дисперсии в кубическом кристалле свинца.

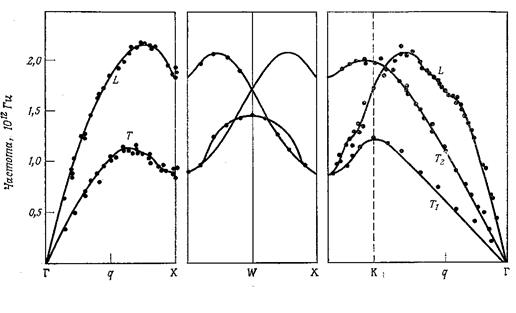
На оси абсцисс отмечены точки высокой симметрити для волнового вектора в зоне Бриллюэна. Сплошные кривые – теоретические результаты, точки – эксперимент.

Понятие о фононах

Энергия колебаний решётки, или энергия упругой волны, является квантовой величиной. Квант энергии упругой волны называется фононом, названный так по аналогии с фотоном – квантом электромагнитной волны. Рассмотрим некоторые элементы квантовой теории гармонического кристалла сначала в одномерном случае. Тогда для классической функции Лагранжа L можно записать такое выражение

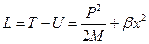. (5.5.1)

Что бы получить функцию Гамильтона, необходимо импульс P, заменить дифференциальным оператором который действует на функцию состояния системы, тогда получаем

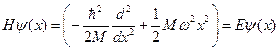. (5.5.2)

Решения этого дифференциального уравнения хорошо известны. Собственные значения энергии для кристалла определятся фрмулой

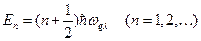, (5.5.3)

где 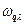– частота нормальных колебаний, n – квантовое число. Таким образом, каждое нормальное колебание атомов в решётке происходит с энергией равной энергии осциллятора, имеющего массу, равной массе атома, и колеблющегося с частотой, равной частоте нормального колебания. Для трёхмерного кристалла полная энергия колебательного движения запишется (с учётом поляризации) в виде

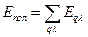(5.5.4)

Таким образом, полная энергия кристалла, состоящего из N атомов, равна энергии 3 N независимых осцилляторов.

Ранее мы уже рассмотрели некоторые свойства колебаний линейных одноатомной и двухатомной цепочек. Наиболее характерным свойством этих колебаний является их закон дисперсии, связывающий частоту с волновым вектором 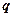. И так как, волновые числа, отличающиеся на вектор обратной решётки эквивалентны, то и частоты, суть периодические функции с периодом обратной решётки.

В зависимости от степеи возбуждения нормального колебания оно может испускать то или иное число одинаковых фононов. Так, если, например, n=3, то его энергия 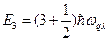, т.е. имеем три одинаковых фонона. Отсюда можно сделать заключение, что система фононов, есть система с переменным числом частиц. А для описания таких систем квантовая механика использует,как правило, аппарат вторичного квантования. Приведём элементы этого аппарата для одномерного осциллятора. Воспользуемся формулой (5.7.2) и запишем гамильтониан в таком виде

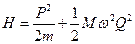, (5.5.5)

где 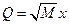. Структура того гамильтониана упростится, если ввести два новых оператора, называемых операторами рождения b и уничтожения 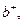частиц следующими соотношениями

и 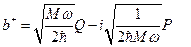. (5.5.6)

Из канонических перестановочных соотношений следует, что .

Операторы 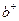и 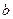– называются Бозе операторами рождения и уничтожения частиц. Теперь функция Гамильтона H в представлении операторов рождения и уничтожения, может быть преобразована к виду

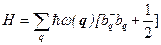, (5.5.7)

Основное состояние кристалла описывается функцией в обозначении Дирака 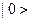. В этом состоянии энергия

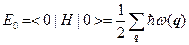(5.5.8)

Имеет наименьшее значение. Итак, стационарные возбуждённые состояния кристалла распределены по всему кристаллу и характеризуются волновым вектором q, (следовательно, квазиимпульсом 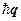и энергией 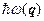). Эти возбуждённые состояния называются фононами.

Энергия же кристалла в состоянии пределяется согласно функции Гамильтона выражением

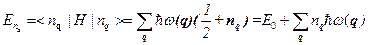(5.5.9)

Второе слагаемое в этом выражении описывает энергию возбуждения системы.

Различным возбуждённым состояниям при этом соответствует различный набор чисел , причём энергия возбуждения увеличивается с возрастанием значений этих чисел. Формально выражение для энергии возбуждения имеет вид полной энергии идеального газа, состояния частиц которого задаются квазиволновым вектором q. При этом число частиц в этом состоянии есть квантовое число соответствующего осциллятора . Представление о таком идеальном газе очень удобно: оно позволяет наиболее простым и наглядным образом выразить то обстоятельство, что энергия колеблющейся решётки может изменяться не произвольно, а только порциями – квантами - величины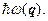

Полное число фононов в кристалле, конечно, не сохраняется: оно даётся суммой всех и может быть любым. Число фононов в каждом произвольном состоянии так же произвольно. Это означает, что газ фононов подчиняется статистике Бозе – Эйнштейна. При этом следует помнить, что химический потенциал фононного газа равен нулю: так как число фононов не постоянно и определяется при термодинамическом равновесии из условия минимума энергии, что как раз и определяет химический потенциал. В этом случае распределение Бозе-Эйнштейна превращается в формулу Планка

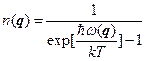.(5.5.10)

Это соотношение вместе с законом дисперсии позволяет вычислять среднюю энергию колебаний решётки, и, следовательно, остальные термодинамические характеристики по известным формулам идеального газа.

Таким образом, при описании малых колебаний атомов решётки имеется два эквивалентных языка: язык гармонических осцилляторов и язык фононов. В связи с фононным языком описания сделаем следующие замечания: первое, бездоказательно был введён квазиимпульс фонона в виде 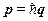. Однако, рассматривая только идеальный газ, мы не можем решить вопрос о существовании или отсутствии квазиимпульса у фонона. Действительно, он определяется по свойству сохраняться (с точностью до 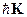, K – вектор обратной решётки), либо в периодическом поле, либо в сумме по всем частицам при взаимном рассеянии, Но в идеальном газе никакие процессы рассеяния не происходят. Эта задача решается рассмотрением рассеяния фононов на объектах, квазиимпульс которых уже определён (например, на электронах или дырках).

Во-вторых, аналогию между частицами идеального газа и фононами можно провести, всё - же, не до конца. Именно, частицы - атомы или молекулы газа представляют собой «самостоятельные» объекты: можно например, поставить вопрос о физическом выделении некоторого их числа. В то время как представление о фононах - это лишь язык для описания нормальных колебаний решётки. Они представляют собой коллективные движения всех атомов кристалла. Поэтому фононы существуют лишь постольку, поскольку существует сама система из атомов, молекул. По этой причине фононы, как и дырки, называют квазичастицами.

В-третьих, представление об идеальном газе фононов возникло на основании выражения (5.5.4) для полной энергии. Однако, оно справедливо только в гармоническом приближении: предполагалось, что потенциальную энергию можно представить в виде квадратичной формы по смещениям атомов. При учёте следующих членов в разложении, т.е. ангаромоническое приближение, появляются члены с третьей и более высокими степенями разложения по отклонениям. Эти дополнительные слагаемые можно трактовать как энергию взаимодействия фононов и газ становится неидеальным, и следует учитывать процессы рассеяния фононов друг на друге.

Не нашли, что искали? Воспользуйтесь поиском: