Статистическая теория ближнего порядка

Как мы уже отмечали, возникновение ближнего порядка обусловлено неравенство энергии взаимодействия для различных пар атомов. Это неравенство порождает зависимрсть энергии твёрдого раствора не только от состава сплава, но и от взаимного расположения разноимённых атомов. Одновременно от состава и взаимного расположения атомов будет зависеть и энтропия твёрдого раствора. Равновесный ближний порядок будет определяться минимумом свободной энергии. В этом параграфе мы рассмотрим основы статистической теории ближнего порядка и получим связь между энергетическими характеристиками упорядочения, введёнными как параметры теории, и параметрами ближнего порядка.

Наибольший прогресс в статистической теории ближнего порядка достигнут в модели парного взаимодействия. Согласно этой модели энергия твёрдого раствора может быть представлена как сумма энергий взаимодействия пар атомов, которая может быть разбита на две части, зависящую и независящую от расположения атомов. Энергии взаимодействия отдельных пар задаются как параметры теории, они независят от состава, температуры, степени порядка, окружения атомов, амплитуды и характера колебаний атомов.

Если – энергия взаимодействия между атомами A и B, находщимися в узлах n – и – узлах кристалла, и – соответственно энергии для пар AA и BB, то энергией упорядочения называют величину

. (8.10.1)

Отметим, что иногда под энергией понимается вдвое большая величина, указанная здесь или отличающаяся от неё знаком. В простейшем рассмотрении энергии упорядочения отличны от нуля лишь для ближайших соседей, однако для большинства твёрдых растворов, как правило, и для более удаленных соседей.

Наиболее простым является рассмотрение и на основе приближения, которое называется квазихимическим. Согласно этому приближению учитывается только взаимодействие между атомом, принимаемым за центральный и его ближайшими соседями, причём за центральный принимается поочерёдно каждый атом. В этом приближении внутренняя энергия твёрдого раствора может быть записана в виде

. (8.10.2)

После подстановки сюда соотношений

, (8.10.3)

гдеь 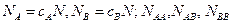– числа пар атомов, соответствуюших сортов получим для энергии твёрдого раствора такое выражение

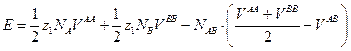. (8.10.4)

Поскольку в теории принимается, что энергия парного взаимодействия не зависит от взаимного расположения атомов, связь энергии твёрдого раствора с параметрами ближнего порядка определяется только множителем . Последний член в (8.10.4), характеризующий изменение энергии системы при образовании твёрдого раствора из механической смеси чистых компонентов, называется энергией смешения

. (8.10.5)

Очевидно в рассматриваемой модели W – энергия упорядочения для ближайших соседей. Равновесные значения числа пар атомов сорта A и B могут быть получены из условия минимума свободной энергии твёрдого раствора

, (8.10.6)

где T – температура, S – энтропия. Конфигурационная часть энтропии определяется таким соотношением , где – постоянная Больцмана, 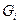– число способов осуществления конфигурации с данной степенью порядка 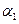, равное числу сочетаний из возможных пар по парам

(8.10.7)

Подстановка формул(5, 7) в выражение 6 позволяет получить уравнение

(8.10.8)

Из этого уравнения заданием энергии упорядочения W для ближайших соседей можно вычислить параметр ближнего порядка .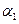

Ближний порядок можно представить и в виде флуктуаций состава или дальнего порядка. В этом случае ближний порядок может характеризоваться отклонением состава или дальнго порядка в данном месте решётки от соответствующих средних значений. Удобно распределение атомов бинарного твёрдого раствора по узлам решётки описывать набором чисел 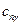, равным единице, если в n – узле – подрешётки находится атом A, и равных 0, если в нём находится атом B. Поскольку вероятность замещения атомами A узлов – подрешётки равна , то – избыточная вероятност замещения узла 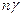атомом сорта A. Заметим, что если в неупорядоченном растворе в элементарной ячейке содержится один атом, индекс может быть опущен. Среднее значение произведения избыточных вероятностей замещения узлов 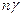атомами сорта A вполне характеризует корреляцию в расположении атомов разного сорта и поэтому называется параметром корреляции

(8.10.9)

Из этого выражения следует, что параметр корреляции равен разности вероятности одновременного пребывания на узлах и атомов A и вероятности в случе хаотического расположения атомов. С учётом (8.9.2)

(8.10.10)

Очень полезным оказывается фурье – представление флуктуаций в расположении атомов следующего вида

(8.10.11)

Суммирование по вектору проводится по всем векторам, лежащим в первой зоне Бриллюэна. Обратное преобразование определяет фурье – коэффициенты этого разложения

Нетрудно проверить, что правая часть этого выражения периодична с периодом обратной решётки, а левая часть, взятая по совокупности векторов n прямой решётки, определяет флуктуационное изменение концентрации атомов сорта A на узлах в этой области. Для неупорядоченного твёрдого раствора с одним узлом в элементарной ячейке нетрудно получить такое соотношение

Здесь учтено, что и соотношение (8.10.9). Снова воспользовавшись фурье – преобразованием из последнего соотношения можно получить такое выражение для фурье – образа параметра ближнего порядка

где – объём элементарной ячейки кристалла твёрдого раствора.

Точно так же можно записать фурье – образ и для энергии упорядочения W

Рассмотренные в этом параграфе теоретические соотношения неоднократно использовались в экспериментальных работах для определения энергий упорядочения как по картине 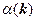, определённой рентгено – или нейтронографически, так и по параметрам .

Не нашли, что искали? Воспользуйтесь поиском: