Радиальные функции распределения межатомных расстояний и атомной плотности. Кристаллическую структуру аналитически мы описывали целочисленными векторами трансляций прямой решётки R

Кристаллическую структуру аналитически мы описывали целочисленными векторами трансляций прямой решётки R. Однако в отсутствие дальнего порядка требуется новый язык. Язык, который прзволял бы ввести в динамические или термодинамические соотношения параметры, оисывающие макроскопические взаимодействия между атомами. Для этой цели незаменимым оказывается формализм атомных функций распределения.

Названные функции представляют собой не что иное, как одночастичную, двух частичную, трёхчастичную и т.д. плотности вероятности, Формально они определяются соотношением

, (9.2.1)

где dP есть вероятность найти атом в объёме d 1 вблизи точки 1, атом в объёмеd 2 вблизи точки 2 и т.д. В большинстве задач достаточно считать, что рассматриваемые функции не зависят от времени, описывая лишь статическую конфигурацию атомов; при этом выборка производится так, что один и тот же атом можно считать дважды, только если вновь попадаешь в одну и туже точку пространства.

На основании предположения о макроскопической однородности образца следует, что средняя плотность атомов в единице объёма должна быть постоянной, т.е.

Независимо от положения точки 1. Интегрируя теперь (9.2.1) по всем координатам, получаем

. (9.2.2)

Вычисления можно упростить, если ввести каноническую функцию распределения, полагая

.

Тогда интеграл кратности s по единичному объёму от функции g равен единице. Другими словами, величина даёт нам вероятность найти именно такой тип расположения s - атомов из всех других возможных способов размещения их в пространстве при одной и той же средней плотности.

Оказывается можно показать, что почти все данные прямых измерений, относящиеся к расположению атомов в конденсированных средах описываются бинарной функцией распределения g(1,2). В случае пространственной однородности системы эта функция может зависеть только от вектора , соединяющего точки 1 и 2, т. е

.

Для идеального кристалла эта функция сводится к набору дельта функций в узлах решётки

(9.2.3)

Т.е. графическая зависимость бинарной функции изображается в виде острых пиков, отвечающих местам расположения атомов. Отсутствие дальнего порядка приведёт в основном к уширению и размытости далёких пиков этой функции в однородный континуум. Масштаб локального порядка можно определить эмпирически как расстояние, за пределами которого функция становится близкой к единице. Однако, вводя, статистические функции распределения, необходимо учесть ориентационный беспорядок, который делает образец макроскопически изотропным. Следовательно, парную фкнкцию (8.2.3) надо усреднять по всем направлениям векторов R. В результате этого мы приходим, к набору концентрических сферических оболочек, радиусы которых равны длинам всех возможных вектров.

В жидкостях атомы не могут находиться на произвольных расстояниях друг от друга, поскольку их упаковка достаточно плотная. Вероятность нахождения некоторого атома, в какой – либо точке объёма V зависит от того, в какой точке находится другой атом. Такая вероятная связь между взаимным расположением атомов (их корреляция) количественно описывается бинарной функцией .

(9.2.4)

Так как жидкости изотропны, то функция g зависит только от взаимного расстояния между парой рассматриваемых атомов

Равенство (7.2.4) можновыразить в иной форме. Для этого совместим начало координат с центром атома номер 1 и опишем вокруг него две концентрические окружности радиуса R и R+dR. Вероятность обнаружения атома 2 в сферическом объёме равна

. (9.2.5)

Очевидно, бинарная функция g удовлетворяет условию нормировки

, (9.2.6)

это условие показывает, что сумма вероятностей нахождения данного атома на всех возможных расстояниях от фиксированного атома, равна единице. Так как силы отталкивания препятствуют взаимному проникновению атомов, то в интервале (r – радиус атома) функция g(R)=0, а если она стремится к единице.

Пусть в слое находится dn атомов. Тогда число атомов в единице объёма этого шарового слоя определится формулой

. (9.2.7)

В различных шаровых слоях число атомов неодинаково, поэтому . Количество атомов в единице объёма может изменяться вследствие миграции атомов между слоями, поэтому dn является средним за время наблюдения. Следовательно,

,

а интеграл равен числу атомов в объёме V, за исключением фиксированного атома. Если это число постоянно, то

. (9.2.8)

Если же число атомов флуктуирует вокруг среднего значения. <N>, как это имеет место вжидкостях, то

. (9.2.9)

В качестве объёма интегрирования принимается сфера радиуса , объём которой достаточнро велик, чтобы содержать большое число атомов. При этом предполагается, что атомы, расположенные вблизи поверхности сферы, имеют то же окружение, что и атомы, расположенные в центре. Последние два выражения определяют условия нормировки для функции атомной плотности. Первое из них – является точным для кристаллов, второе для – жидкостей. Используя (8.2.6) и (9.2.8), найдём

,(9.2.10)

где – среднее число атомов в единице объёма.

Согласно этому соотношению значения g(R) равны отношению истинного количества атомов в единице объёма к средней атомной плотности. Поэтому g(R) имеет смвсл относительной радиальной функции распределения. Она является важнейшей характеристикой структуры атомарных жидкостей и аморфных тел. Исследованию этой функции было посвящено очень много как теоретических, так и экспериментальных работ. Самые точные данные получаются при исследовании дифракции нейтронов и рентгеновских лучей: вместе с тем эти данные никогда не удаётся интерпретировать однозначно особенно в тех случаях, когда в рассеяние вносят вклад несколько различных элементов. Однако даже в благоприятном случае одноатомного материала всё, что мы можем измерить, – это радиальную функцию распределения. На рис. представлены некоторые характерные черты этой функции.

Что можно извлечь из этой фунукции? Как показывает рисунок, она имеет некоторые «черты», допускающие физическую интерпретацию. В частности, эта функция должна обратиться в нуль на расстоянии равном диаметру атомного остова; затем она возрастает, достигая максимума (пика) на некотором характерном расстоянии 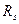. Это расстояние обычно отождествляют с радиусом первой координационной сферы атомов. Площадь под этим пиком

(9.2.11)

Есть координационное число данной структуры; если предположить ковалентные тетраэдрические связи, то число ближайших соседей должно быть равно z = 4. Аналогично, следующий пик обусловлен второй координационной сферой и т. д. Однако, фактически координационное число не известно. А число атомов внутри каждой сферы становится всё более и более неопределённым по мере того, как пики уширяются, сливаются друг с другом, а затем вообще теряются на фоне континуума где . Для многих теоретических задач удобнее измерять функцию g(R) по отношению к этому фону, полной корреляционной функцей h(R)

. (9.2.12)

Эта функция характеризует степень локального отклонения от статистической однородности вблизи данного атома. Тогда размер области упорядочекния в этом случае определяется эмпирически как расстояние на котром h(R) обращается в нуль. В связи с проблемой выяснения окружения данного атома в жидкости. Сделаем такие разъяснения. Большинство кристаллов характеризуется сравнительно плотной упаковкой. Считая атомы шарами, можно утверждать, что в рамках основных свойств симметрии решётки или ограничений накладываемых связью, каждый атом «касается» возможно, большего числа соседей. Однако атомы – шары даже в гранецентрированной или гексагональной плотноупакованных решётках не заполняют весь объём кристалла. Как же быть с междоузельными областями? В случае кристаллических тел каждому атому мы сопоставляем многогранник – ячейку Вигнера – Зейтца, которая обладает максимальной симметрией точечной группы кристалла и позволяет строить кристаллическую решётку из них без промежутков между ячейками. Структура многих неупорядоченных систем так же близка к наиболее плотной из всех возможных – с прежними ограничениями геометрической или химической природы. Способ построения ячейки Вигнера – Зейтца для неупорядоченных систем даёт нам теперь систему полиэдрв Вороного (см. рис.). Их уже нельзя считать регулярными и идентичными друг другу; однако, поскольку каждый из них содержит по сферическому атому, полученная ячейка не может слишком сильно отличаться от симметричной ячейки Вигнера – Зейтца. Поэтому окружение каждого атома (или молекулы) в неупорядоченной фазе, в конечном счёте, не должно сильно отличаться от того, которое было бы в регулярном кристалле с той же самой средней плотностью.

Нахождение функции распределения для той или иной жидкости является важнейшей задачей структурного анализа. Количественными параметрами структуры являются координационные числа, равновесные межатомные расстояния, средние квадратичные смещения атомов, а также расстояния, на которых исчезает корреляция в расположении частиц.

Дж. Кирквуд нашёл явный вид функции теоретически, исходя из общих принципов статистической механики. Иммитируя атомы твёрдыми взаимодействующими шариками, он получил такую формулу

, (9.2.13)

где – постоянные параметры. Например, для аргона .

Нетрудно увидеть, что эта функция, обладает такой же завиимостью от R, как и экспериментально определяемые функции распределения для одноатомных плотноупакованных жидкостей.

Не нашли, что искали? Воспользуйтесь поиском: