Решение уравнения для бинарной функции распределения

Для иллюстрации изложенного выше, рассмотрим два примера.

1. Система невзаимодействующих частиц. Пусть имеется система, атомы которой имитируются твёрдыми шариками диаметра a. Силы отталкивания в этой модели аппроксимируются непрницаемостью шариков. Силы притяжения отсутствуют, их действие заменяется введением объёма V, ограничивающего движение шариков и обеспечивающего нужную плотность. По своим свойствам такая система напоминает сжатый газ. Потенциальная энергия взаимодействия шариков представляется в виде

.

Уравнение Боголюбова преобразуется к виду

. (9.5.1)

Результаты расчёта бинарной функции расапределения для двух плотностей представлены на рис.

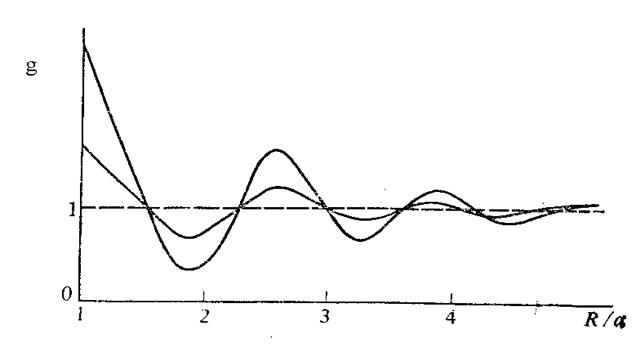Видно, что проходит ряд максимумов и минимумов. По мере увеличения плотнсти всё отчётливее проявляется характерный для жидкости ближний порядок в расположении частиц. Резкость первого пика обусловлена непроницаемостью шаров. Отметим, что задача о системе не взаимодействующих частиц не может привести к результатам, совпадающим с экспериментальными данными. Тем не менее, даже такая модельная задача правильно отражает специфику ближнего порядка в конденсированной системе.

2. Система взаимодействующих частиц. Решение уравнения Боголюбова с учётом взаимодействия наталкивается на серьёзные математические трудности из-за сложности выражения для потенциала сил взаимодействия частиц. Задачу до конца можно решить, если воспользоваться потенциалом Леннарда – Джонса: , если R < a, и

, (9.5.2)

если R>a. В этом приближении при R<a атомы системы снова рассматриваются как непроницаемые шарики. Решение с потенциалом Леннарда – Джонса было выполнено Кирквудом. Резуьтаты расчёта бинарной функции распределения представлены на рисунке и удовлетворительно совпадают с экспериментальными значениями для жидкого аргона.

Найденная функция распределения для аргона была использована для расчёта величины газообразного аргона в зависимости от плотности, при фиксированной температуре исходя из уравнения состояния

.

Оказалось, что при малых плотностях согласие между теорией и экспериментальными значениями удовлетворительно, но при высоких плотностях значение этой величины меньше экспериментальных. Таким образом, уравнение (9.4.11) позволяет найти бинарную функцию распределения и вычислить с её помощью некоторые термодинамические величины, которые не очень хорошо согласуются с экспериментальными данными. Основной недостаток этого видится в грубости суперпозиционного приближения. Предпринимались попытки его улучшения, однако они не привели к удовлетворительным результатам. Поэтому для изучения жидкостей оно не получило широкого рспространения. Наиболее успешный подход состоит в применении полной функции распределения (9.2.12).

Не нашли, что искали? Воспользуйтесь поиском: