Применение дифференциала

Рассмотрим для примера функцию

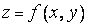
от двух переменных, которую будем предполагать дифференцируемой.

Мы хотим вычислить эту функцию в точке , где

,

,

Приближенные значения этих чисел запишем в виде конечных десятичных дробей

,

.

Таким образом, имеют место приближенные равенства

с абсолютными погрешностями приближения, удовлетворяющими неравенствам

.

Подставив в функцию вместо соответственно , получим приближенное равенство

с абсолютной погрешностью

,

которую при достаточно малых можно приближенно заменить дифференциалом функции в точке :

.

Отсюда получаем неравенство

. (1)

На самом деле это неравенство приближенное, потому что мы получили его, пренебрегая некоторой величиной, правда, значительно меньшей, чем .

Обратим внимание на тот факт, что конечные десятичные дроби при уменьшении , становятся все более и более громоздкими. Поэтому при вычислении числа мы должны беспокоиться не только о том, чтобы оно приближало должным образом, но и чтобы производимые при этом вычисления совершались возможно, экономно. В силу этого замечания из неравенства (1) следует, что если нужно, чтобы абсолютная погрешность не превышала данную малую величину, которую мы обозначим через , то этого мы достигнем, взяв числа , 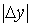такими, чтобы выполнялись неравенства

, (2)

т. е. чтобы погрешность распределялась между слагаемыми в правой части неравенства (1) поровну.

Из неравенств (2) видно, что вычисления будут наиболее экономными, если в качестве , (на самом деле , ) взять наибольшие возможные числа, удовлетворяющие этим неравенствам.

П р и м е р 1. Функция имеет для , непрерывные частные производные, равные

.

Поэтому приближенное равенство

имеет абсолютную погрешность, которая при малых приращениях , если пренебречь величинами, значительно меньшими этих приращений, удовлетворяет неравенству

.

Если требуется, чтобы гарантированная погрешность была меньше , надо подобрать так, чтобы

.

Мы видим, что числа не обязательно должны быть равными. Если, например, значительно меньше, чем , то соответственно надо взять меньшим, чем . Иначе наши вычисления были бы неэкономными. Если бы, например, было, что

,

где , то оказалось бы, что

,

и при этом на вычисление второго слагаемого , ввиду излишней малости , мы потратили бы излишнюю работу. Между тем вычисления упростятся, если взять возможно большие , , удовлетворяющие неравенствам.

.

П р и м е р 2. Функция имеет непрерывные частные производные , . Поэтому приближенное равенство

имеет абсолютную погрешность , которая при малых приращениях , если пренебречь величинами, значительно меньшими этих приращений, удовлетворяет соотношениям

.

Соответственно относительная погрешность удовлетворяет соотношениям

.

Мы видим, что при малых и можно считать, что относительная погрешность произведения не превышает сумму относительных погрешностей сомножителей.

П р и м е р 3. Функция для имеет непрерывные частные производные

.

Поэтому приближенное равенство

имеет абсолютную погрешность , которая при малых приращениях , если пренебречь величинами, значительно меньшими, чем , удовлетворяет соотношениям

.

Соответственно относительная погрешность удовлетворяет соотношениям

.

Таким образом, при малых и можно считать, что относительная погрешность частного не превышает сумму относительных погрешностей делимого и делителя.

29 Таблица основных неопределённых интегралов.

Таблица основных неопределенных интегралов

33 Нахождение площадей плоских криволинейных фигур.Длина дуги.Объём тела вращения.

18.1.1. Площадь плоской фигуры в декартовых координатах

а) Допустим, что фигура предполагает наличие границы

является криволинейной трапецией и , при условии, что на

Если находится ниже оси (рис. 18.1), то

Рис. 18.1

Пример:

(рис. 18.1, б).

б) Предположим, что для фигуры харакерно наличие границы Площадь (рис. 18.2, а),

Рис. 18.2

соответственно получаем формулу

В общем случае площадь находится с помощью формулы

Пример:

(рис. 18.2, б).

Не нашли, что искали? Воспользуйтесь поиском: