Разложение в степенные ряды основных элементарных функций.Формула Моавра.

Из дифференциального исчисления известно, что если функция f(x) имеет в некоторой окрестности производные до порядка n включительно, то можно написать формулу Тейлора для этой функции. Положим при любом n = 1, 2,…

и Если

(1.1)

то ряд

сходится и его суммой будет функция f(x).

Определение 1.1. Представление функции f(x) в виде ряда

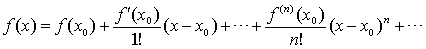(1.2)

называется разложением этой функции в ряд Тейлора.

Определение 1.2. Разложение функции f(x) в ряд Тейлора при x₀=0

(1.3)

называется разложением этой функции в ряд Маклорена.

Подчеркнем, что из сходимости ряда Тейлора для функции f(x) еще не следует его сходимость именно к этой функции, поэтому при разложении функции в ряд Тейлора следует проверять соблюдение условия (1.1).

Теорема 1.1. Пусть

(1.4) где стоящий справа ряд сходится в некотором отрезке к функции f(x). Тогда этот ряд является рядом Тейлора, то есть

(1.5)

Доказательство. Применим к равенству (1.4) п раз теорему о почленном дифференцировании степенного ряда. Тогда получим

Если в этом тождестве положить x=x₀, то все слагаемые справа, кроме первого, обратятся в нуль и получим откуда и следует (1.5). Теорема доказана.

2. Разложение основных элементарных функций.

Теорема 2.1. Если функция f(x) определена и имеет производные сколь угодно высоких порядков и существует постоянная, такая, что при лю­бых х и п удовлетворяет неравенству 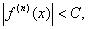то функция f(x) разлагается в ряд Тейлора (1.2) при любом x₀.

Приведем без доказательства следующие разложения элементарных функций в ряд Маклорена

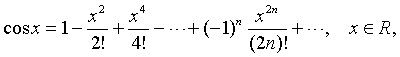
это разложение имеет место при любом натуральном значении и любом значении x, если число не является натуральным, то данное равенство справедливо лишь при –1< x <1;

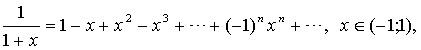
Формула Муавра для комплексных чисел утверждает, что

для любого

Формула Муавра сразу следует из формулы Эйлера и тождества для экспонент , где b — целое число.^[1]

Аналогичная формула применима также и при вычислении корней n -ой степени из ненулевого комплексного числа:

где k = 0, 1, …, n —1.

Из основной теоремы алгебры следует, что корни n -й степени из комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n -угольника, вписанного в окружность радиуса 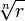с центром в нуле.

Не нашли, что искали? Воспользуйтесь поиском: