Понятие дифференцируемости функции двух переменных

Определение 26.3.

Пусть определена функция 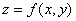, тогда

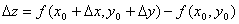- полное приращение функции.

Определение 26.4.

Пусть функция 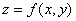определена в окрестности точки .

Функция 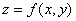называется дифференцируемой в точке , если ее полное приращение в этой точке может быть представлено в виде:

(26.1),

где -константы, -бесконечно малые функции при .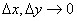

Теорема 26.1.

Если функция 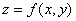дифференцируема в точке , то она непрерывна в этой точке.

Доказательство.

Очевидно из (26.1): .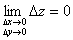

Теорема 26.2 (необходимое условие дифференцируемости).

Если функция 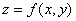дифференцируема в точке 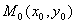, то она имеет в этой точке частные производные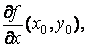 , причем:

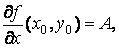
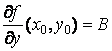. (26.2)

Доказательство.

Пусть имеет место формула (26.1).

Положим ,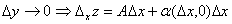

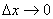где при - бесконечно малая функция.

Разделив на , и переходя к пределу при 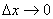, получим:

,

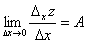то есть частная производная по переменной 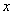существует и равна .

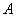Второе равенство доказывается аналогично.

Замечание 1. Из непрерывности не следует ее дифференцируемость!

Пример 26.2.

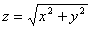непрерывна в точке (0,0), но 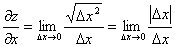не существует.

Аналогочно, не существует частной производной по 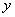. Следовательно, функция не дифференцируема.

Замечание 2. Из существования частных производных не следует дифференцируемость функции.

Пример 26.3.

Функция 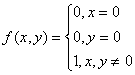имеет частные производные в точке (0,0),

но не является в этой точке непрерывной, следовательно –

не дифференцируема.

Теорема 26.3 (достаточное условие дифференцируемости).

Если функция 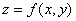имеет частные производные в некоторой окрестности точки 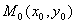и эти производные непрерывны в самой точке 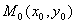, то функция дифференцируема в точке .

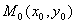Следствие.

Если частные производные непрерывны, то функция непрерывна.

Определение 26.5.

Если функция 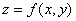дифференцируема в точке 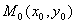, то дифференциалом 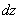называется линейная относительно приращений часть полного приращения этой функции в точке 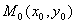, т.е.

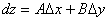, или

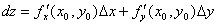(26.3)

Дифференциалами независимых переменных называются их приращения

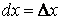
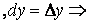
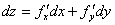(26.3’)

Не нашли, что искали? Воспользуйтесь поиском: