Разностные схемы, аппроксимирующие уравнения фильтрации упругой жидкости

Из математического анализа известно, что дифференциальные операторы при дискретном изменении аргументов не определены. Для отыскания решений в этом случае необходимо исходные дифференциальные уравнения заменить на их дискретные аналоги.

В качестве примера рассмотрим построение дискретных аналогов краевой задачи для одномерного уравнения теплопроводности:

(1)

при ; при ;

при ; при ;

Напомним, что уравнение этого типа описывает распределение давления в однородном пласте при упругом режиме фильтрации слабосжимаемой жидкости. Разделим отрезок на М одинаковых частей точками (), отстоящими одна от другой на расттоянии 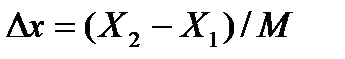(рис. 4). Выразим производную через значения функции в дискретных точках ; при этом будем использовать обозначения .

Известно несколько способов построения дискретных аналогов (разностной аппроксимации) производных. Наиболее распространенный способ основан на использовании метода разложения функций в ряд Тейлора. Запишем выражение ряда Тейлора для функции в окрестности точки пр положительном приращении аргумента:

.

То же выражение в индексном обозначении имеет вид

где ;

Аналогично записывается разложение при отрицательном приращении аргумента;

.

Из первого разложения можем получить выражение для первой производной – правую разность

Из второго разложения можем получить выражение для левой разности

Наконец, вычтя второе разложение из первого, получим центральную разность

Просуммировав оба исходных разложения, после несложных преобразований получим аппроксимацию второй производной

(2)

Используем полученную аппроксимацию второй производной. Построим дискретный аналог краевой задачи (1). Для этого область решения заменим совокупностью равностоящих прямых , где (рис. 4), составляющих аналог области: Заменим в исходном уравнении вторую производную её дискретным аналогом. Частная производная по времени обычно заменяется односторонней разностью

Введя для удобства обозначения

, ,

можно записать

.

Следовательно, рассматриваемое дифференциальное уравнение упругого режима в конечно – разностной форме сводится к системе уравнений

(3)

Дискретный аналог начального условия строится достаточно просто и записывается в виде

, (4)

По аналогичной схеме строятся дискретные аналоги граничных условий первого рода:

при

при (5)

Более сложным является вопрос о построении дискретных аналогов граничных условий, в состав которых входят производные. Пусть, например, одно из граничных условий задано в виде

При (6)

что физически означает непроницаемость границы Дискретный аналог условия (6) можно построить несколькими способами. Наиболее удобный основан на использовании метода отражения. При его реализации в рассмотрение дополнительно вводится точка за пределами области решения . Представляя дискретный аналог первой производной по схеме центральных разностей, получим

.

На этом основании дискретный аналог условия (6) можно представить в виде

(7)

Как видно из приведенной записи, исходная краевая задача для дифференциального уравнения в конечно-разностной постановке сводится к системе алгебраических уравнений и тем самым существенно упрощается. В таком упрощении заключается все преимущества метода конечных разностей.

Осн.: 4. [279-287]. 8. [11-33].

Доп.: 12. [18-113].

Контрольные вопросы:

1. Что такое дискретный аналог непрерывной области?

2. Что такое шаблон?

3. Что такое разностная схема дифференциального уравнения?

Не нашли, что искали? Воспользуйтесь поиском: