Лекция 15. Решение системы конечно-разностных уравнений. Сходимость метода.

После дискретизации области и построения дискретного аналога краевой задачи необходимо оценить сходимость конечно-разностного решения к точному решению исходной задачи, а также получить конечно-разностное решение, т.е. решить систему конечно-разностных уравнений. Реализация этих двух этапов представляет основные принципиальные трудности при практическом использовании метода конечных разностей.

Говорят, что разностное решение сходится к решению задачи если норма разности этих решений в узлах сетки стремится к нулю при стремлении к нулю шагов дискретизации:

при

В зависимости от свойств искомых функций и решаемых задач в качестве норм могут приниматься различные величины (максимум абсолютных величин разностей, средняя квадратичная разность).

Конечно-разностное решение представляет практический интерес только в том случае, если имеет место его сходимость к точному решению. Непосредственная проверка сходимости разностных схем вызывает большие затруднения. В теории разностных схем доказывается, что схема, которая аппроксимирует исходную задачу и устойчива, является сходящейся. Исследования аппроксимации и устойчивости оказываются относительно более простыми.

Трудности решения системы конечно-разностных уравнений в первую очередь обусловлены её большой размерностью, равной числу дискретных точек, в которых ищутся значения функций. Размерность системы можно уменьшить увеличением шага дискретизации. Однако этот путь приводит к потере точности, и им нельзя пользоваться без достаточного обоснования.

При фиксированной размерности трудоемкость зависит от типа разностной схемы. Поясним это на примере системы уравнений (3), где во втором слагаемом вместо индекса, указывающего номер временного шага, пока проставлены звездочки. Рассмотрим два варианта:

(8)

(9)

Совокупность узлов, участвующих в разностных схемах, можно изобразить схематично в виде так называемых шаблонов. Для первой и второй схем соответственно шаблоны имеют вид, представленный на рис. 5.

Рис. 5. Шаблоны для явной (а) и неявной (б) схем

Первая схема называется явной. Как наглядно видно из шаблона, в этой схеме каждое значение искомой функции на (n+1) – м временном слое индивидуально определяется через три значения функции на предыдущем n –м слое.

Разрешив (8) относительно , получим

Используя начальные условия, т.е. значения функции на нулевом слое, довольно просто можно вычислить последовательно значения функции на любом последующем временно слое. Но явная схема имеет очень существенный недостаток: она оказывается сходящейся только при соблюдении ограничительного условия

,

т.е. условно устойчива.

Вторая схема называется неявной. Она сходится при любом отношении шагов. Но, как видно из шаблона, непосредственно вычислить индивидуальное значение функции на (n+1) –м слое по известным значениям на n-м слое нельзя. На каждом слое нужно полностью решать всю систему уравнений.

Как уже подчеркивалось раньше, система конечно-разностных уравнений является алгебраической, поэтому к ней применимы известные методы решения алгебраических уравнений. В то же время отметим, что каждое неявное конечно-разностное уравнение содержит только три значения искомой функции в соседних узлах. Вследствие этого матрица коэффициентов системы конечно-разностных уравнений

a b 0 0 0

b a b 0 0

0 b a b 0

……………..

0 b a b

0 b a

где , , а все элементы, не лежащие на трех выделенных диагоналях, равны нулю. Для решения систем уравнений подобного вида разработаны специальные методы, среди которых одним из наиболее популярных является метод прогонки.

Рассмотрим его на примере решения системы (9) с начальными и граничными условиями (4), (5), (7). Для удобства перепишем уравнение в развернутом виде

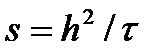, (10)

Будем считать, что значения функции в соседних узлах связаны между собой соотношениями

(11)

(12)

Подставив (12) в (10), получим

,

откуда следует

(13)

Сравнивая (13) с (11), получаем соотношения

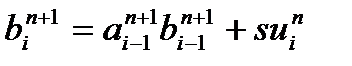, (14)

которые по известным значениям , позволяют вычислить , .

Для узла уравнение (10) и соотношения (11) имеют вид

(15)

(16)

Используя граничные условия (5) из (15) получим

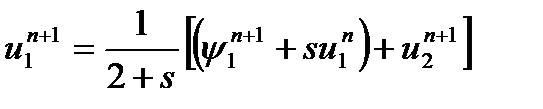(17)

и далее в результате сопоставления равенств (17) и (16) имеем

; (18)

Соотношения (18) и (14) позволяют последовательно рассчитать пары коэффициентов (), (), …., ().

Эта процедура известна как «прямой ход»

Используя найденные значения пар коэффициентов и второе из граничных условий (5), с помощью (11) можем вычислить искомые значения функции во всех узлах, начиная с :

; ,......

В этом состоит операция «обратный ход».

Повторяя «прямой» и «обратный» ходы на каждом последующем временном шаге, найдём численное решение задачи в любом заданном интервале изменения времени.

Метод прогонки удобен тем, что требует относительно небольших объёмов оперативной памяти и затрат машинного времени на проведение расчётов.

Осн.: 4. [279-287]. 8. [11-33].

Доп.: 12. [18-113].

Контрольные вопросы:

1. Что такое разностная схема дифференциального уравнения?

2. Что такое явная схема?

3. Что такое неявная схема?

4. Условие сходимости разностной схемы

Не нашли, что искали? Воспользуйтесь поиском: