Построение кольцевых маршрутов

Коммерческая деятельность обычно связана с командировками, поездками по городам для заключения сделок. Расстояния между любой парой множества из п городов известны и составляют (i= ;j = ), Если прямого маршрута между городами / и у не существует, то допускают, что = .

Коммерсант, выезжая из какого-либо города, должен посетить все города, побывав в каждом из них один и только один раз, и вернуться в исходный город. Необходимо определить такую последовательность объезда городов, при которой длина маршрута была бы наименьшей.

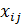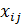Экономико-математическая постановка этой задачи может быть представлена как задача целочисленного линейного программирования. Переменные определим следующим образом: = 1, если коммивояжер переезжает из города i в город j (i = ); в противном случае =0.

Задача заключается в определении матрицы целых неотрицательных значений переменных 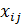, минимизирующих целевую функцию вида:

при ограничениях:

1) для въезда в город j только один раз:

2) для выезда из города i только один раз:

В такой постановке задача коммивояжера представляет собой задачу целочисленного линейного программирования. Действительно, условия = исключают в оптимальном решении значения 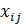= 1 как не имеющие смысла, а ограничения требуют:

1) чтобы маршрут включал только один въезд в каждый город;

2) чтобы маршрут включал лишь один выезд из каждого города, а

целевая функция включала длину маршрута коммивояжера;

3) чтобы маршрут образовывал контур, проходящий через все города.

Таким образом формируется экономный вариант маршрута

в виде кольца.

Специальная часть

Не нашли, что искали? Воспользуйтесь поиском: