Расчет прочности изгибаемых железобетонных элементов по сечениям, нормальным к продольной оси.

Проверку прочности нормальных сечений изгибаемых железобетонных элементов производят из условия:

M_Sd £ M_Rd,

где: M_Sd – расчетный момент в рассматриваемом сечении, вызванный действием внешних нагрузок;

M_Rd – предельный момент, воспринимаемый сечением при заданных геометрических размерах, прочностных характеристиках бетона, количестве и размещении арматуры.

Прочность изгибаемых железобетонных элементов имеющих как минимум одну плоскость симметрии и изгибаемых в этой плоскости (рис.8.2) следует проверять из условия M_Sd £ M_Rd, где:

M_Rd = a f_cd A_cc + f_yd A_s2 (d – c₁)

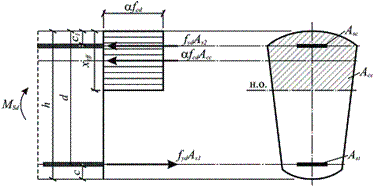
Рис. 8.2. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси изгибаемого железобетонного элемента

При этом высота условной сжатой зоны x_eff определяется из условия

f_yd A_s1 = a f_cd A_cc + f_yd A_s2,

При расчете элементов, имеющих полку в сжатой зоне сечения, следует ограничивать значение ее расчетной ширины b_eff из условия, что размер свеса полки в каждую сторону от ребра должен быть не более величин, указанных в главе 7 СНБ 5.03.01-02.

Расчет железобетонных изгибаемых элементов прямоугольного сечения (сечением b_w×h) следует производить из условия M_Sd £ M_Rd, где:

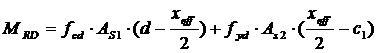
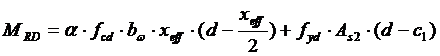
При этом высоту условной сжатой зоны x_eff определяют из условия

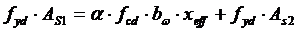
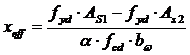
Расчет железобетонных изгибаемых элементов таврового и двутаврового сечений, имеющих полку в сжатой зоне сечения, следует производить следующим образом:

- если граница сжатой зоны проходит в пределах высоты полки (рис. 8.3а), т.е. соблюдается условие:

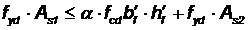
расчет производится как для прямоугольного сечения шириной, равной ширине полки b_f^/, по формуле:

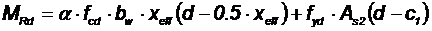
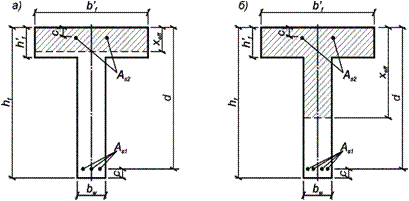
Рис. 8.3. Положение границы условной сжатой зоны в сечении изгибаемого железобетонного элемента таврового сечения

а) в полке; б) в ребре

- если граница сжатой зоны проходит в ребре (рис. 8.3б), т.е. условие не соблюдается, расчет производится из условия M_Sd £ M_Rd, где:

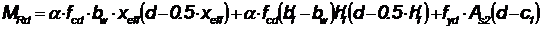
При этом высоту сжатой зоны x_eff следует определять по формуле

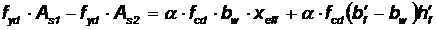
Формулы действительны при x_eff≤ξ_lim·d, Для элементов выполненных из бетона классов С25/30 и ниже с арматурой классов S240, S400 и S500 при x_eff>ξ_lim·d допускается производить расчет из указанного условия принимая x_eff=ξ_lim·d.

При расчете внецентренно сжатых элементов следует различать два случая:

— случай большого эксцентриситета, когда x_eff /d £ x_lim (рис. 8.4);

— случай малого эксцентриситета, когда x_eff /d > x_lim (рис. 8.5).

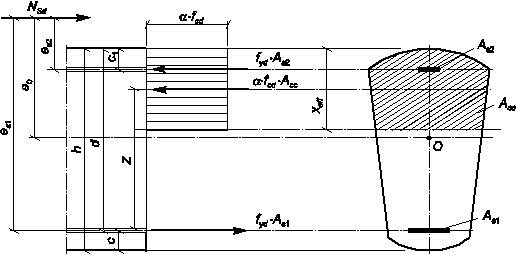
Рис. 8.4. Схема усилий и эпюра напряжений в сечении, нормальном

к продольной оси внецентренно сжатого железобетонного элемента

(случай большого эксцентриситета)

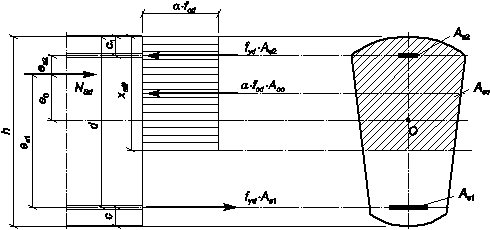
Рис. 8.5. Схема усилий и эпюра напряжений в сечении, нормальном

к продольной оси внецентренно сжатого железобетонного элемента

(случай малого эксцентриситета)

Расчет внецентренно сжатых железобетонных элементов по прочности сечений, нормальных к продольной оси, для случая большого эксцентриситета (при x_eff /d £ x_lim) следует производить как для изгибаемых элементов (см. рис. 8.4), принимая

M_Sd = N_Sd×e_{s 1}

а высоту сжатой зоны определять из условия равновесия

N_Sd + f_yd ×A_s1 - f_yd ×A_s2 = a ×f_cd ×A_cc.

При x_eff > x_lim×d расчет допускается производить из того же условия (как для изгибаемых элементов), но при этом высота сжатой зоны для элементов из бетона классов по прочности С²⁵/₃₀ и ниже должна определяться из условия

,

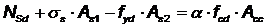где

.

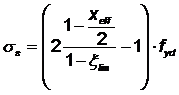Для элементов из бетона классов по прочности выше С²⁵/₃₀ при x_eff > x_lim×d расчет следует производить по деформационной расчётной модели.

В случае, когда расчетная продольная сила N_Sd не превышает 0,08 N_cd (где N_cd = f_cd×A_c), допускается производить расчет внецентренно сжатых элементов по прочности как изгибаемых элементов, без учета продольной силы.

17.Расчет ширины раскрытия трещин нормальных к продольной оси изгибаемого железобетонного элемента.

Предпосылки и допущения при определении ширины раскрытия трещин:

1) В общем случае ширина раскрытия нормальных трещин принимается равной средним деформациям продольной растянутой арматуры на участке между трещинами, умноженным на расстояние между трещинами.

2) Расстояние между трещинами следует определять из условия, по которому разность усилий в растянутой арматуре в сечении с трещиной и в сечении по середине участка между трещинами уравновешиваются силами сцепления арматуры с бетоном. При этом разность усилий в арматуре на этом участке принимается равной усилию, воспринимаемому растянутым бетоном перед образованием трещин.

3) Деформации растянутой арматуры в нормальном сечении с трещиной определяются в общем случае из системы расчетных уравнений деформационной модели железобетонных конструкций (см. главу 6) по заданным значениям изгибающих моментов и продольных сил от соответствующего сочетания внешних нагрузок.

4) Деформации растянутой арматуры допускается определять из упругого расчета нормального сечения с трещиной, принимая условно упругую работу бетона с приведенным модулем упругости и упругую работу арматуры со своим модулем упругости.

5) Для изгибаемых элементов прямоугольного, таврового и двутаврового сечений с арматурой, сосредоточенной у растянутой и сжатой граней элемента, определение деформаций растянутой арматуры в сечении с трещиной допускается производить по упрощенной схеме, рассматривая железобетонный элемент в виде сжатого пояса бетона и растянутого пояса арматуры с равномерным распределением напряжений по высоте сжатого и растянутого поясов.

С учетом принятых предпосылок расчетная ширина раскрытия трещин, нормальных к продольной оси элемента, определяется по формуле

w_k = b×s_rm×e_sm (10.16)

где w_k – расчетная ширина раскрытия трещин;

s_rm – среднее расстояние между трещинами

e _sm – средние деформации арматуры, определяемые при соответствующей комбинации нагрузок;

b – коэффициент, учитывающий отношение расчетной ширины раскрытия трещин к средней.

Коэффициент b выражает отношение максимальной ширины раскрытия трещины w_k к ее среднему значению w_m. Коэффициент вариации отношения w_k/w_m при их изменении от 150 до 400 МПа изменяется незначительно и практически не зависит от напряжений в растянутой арматуре.

Значение коэффициента b рекомендуют принимать равным:

b = 1.7 – при расчете ширины раскрытия нормальных трещин, образующихся от усилий, вызванных соответствующей комбинацией нагрузок, либо от усилий, возникающих при ограничении вынужденных деформаций для сечений, наименьший размер которых не превышает 800 мм;

b = 1.3 – при расчете ширины раскрытия трещин, образующихся от действия усилий, возникающих при ограничении вынужденных деформаций для сечений, наименьший размер которых (высота, ширина, толщина) составляет 300 мм и менее.

Выполняя расчеты ширины раскрытия трещин, образующихся от усилий, вызванных ограничением вынужденных деформаций, для промежуточных размеров сечения элемента значения коэффициента b допускается определять по линейной интерполяции.

Значение средней деформации растянутой арматуры e _sm в формуле (10.16) следует определять:

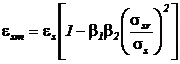, (10.17)

где e _s – деформация растянутой арматуры в сечении с трещиной, определяемая в общем случае из решения расчетной системы уравнений деформационной модели от действия изгибающего момента и продольной силы (см. главу 6);

s _s – напряжения в растянутой арматуре, рассчитанные для сечения с трещиной, от усилий, вызванных расчетной комбинацией нагрузок;

s _sr – напряжения в растянутой арматуре, рассчитанные для сечения с трещиной, от усилий, при которых образуются трещины;

b ₁ – коэффициент, зависящий от условий сцепления арматуры с бетоном и принимаемый равным:

- для стержневой арматуры периодического профиля – 1,0;

- для гладкой стержневой арматуры – 0,5;

b ₂ – коэффициент, учитывающий длительность действия нагрузки, принимаемый равным:

- при действии кратковременных нагрузок – 1,0;

- при действии длительно действующих и многократно повторяющихся нагрузок – 0,5.

Как было показано ранее в формуле (10.17), вместо отношения 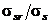допускается принимать:

– при осевом растяжении ;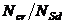

– при изгибе .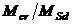

Усилия трещинообразования допускается определять по упрощенным зависимостям как для бетонного сечения по формулам:

M_cr = f_ctm×W_c;

N_cr = f_ctm×A_ct;

где f_ctm – средняя прочность бетона при растяжении

W_c, A_c – соответственно момент сопротивления и площадь бетонного сечения.

Не нашли, что искали? Воспользуйтесь поиском: