Испытания методами микрогидроразрыва

Испытание для определения напряжения создания микротрещины («микро-ГРП» или «микрофрак») определяет наименьшее главное напряжение ин ситу в целевом пласте. Этот тест обычно включает нагнетание жидкости под давлением в небольшой изолированный интервал (4 — 15 футов, 1.2 — 4.6 м) при низких темпах нагнетания (1 — 25 гал/мин, 0.010 — 0.095 м³/мин). Минимальное главное напряжение ин ситу можно определить по спаду давления после закрытия скважины на устье или по нарастанию давления в начале цикла нагнетания. Давление смыкания трещины и давление повторного открытия трещины обеспечивают хорошую аппроксимацию для наименьшего главного напряжения ин ситу.

мини-грп (минифраки)

Самый важный тест на месте проведения работ перед основным ГРП известен как «минифрак» («мини-ГРП»), или испытание для калибровки трещины. Минифрак — это тест с нагнетанием и закрытием скважины на забое, при котором используются полномасштабные скорости нагнетания и относительно большие объемы жидкости, порядка тысяч галлонов (нескольких кубометров). Информация, собираемая при минифраке, включает давления смыкания, , эффективное давление, условия входа в пласт (трение в перфорации и околоскважинной зоне), а также, возможно, признаки ограничения роста трещины в высоту. Участок спада на кривой давления используется для получения коэффициента утечки для данной геометрии трещины. Рис. 7-1 иллюстрирует стратегические участки (точки) на типичной кривой давления, зарегистрированной при проведении калибровки.

Проектирование минифрака должно проводиться вместе с начальным проектированием основной обработки. Цель дизайна минифрака состоит в том, чтобы он был насколько возможно представительным для основного ГРП. Чтобы достичь этой цели, должна быть создана достаточная геометрия, отражающая реальную геометрию основной трещины, а также должны быть получено различимое давление смыкания по кривой спада давления. Наиболее представительный минифрак должен был бы иметь темп нагнетания и объем жидкости такие же, как при основном ГРП, но зачастую это неосуществимо. На самом деле, необходимо найти баланс между несколькими противоречивыми критериями дизайна, включая объем минифрака, создаваемую геометрию трещины, повреждение пласта, разумное время закрытия трещины, а также затраты на материалы и персонал.

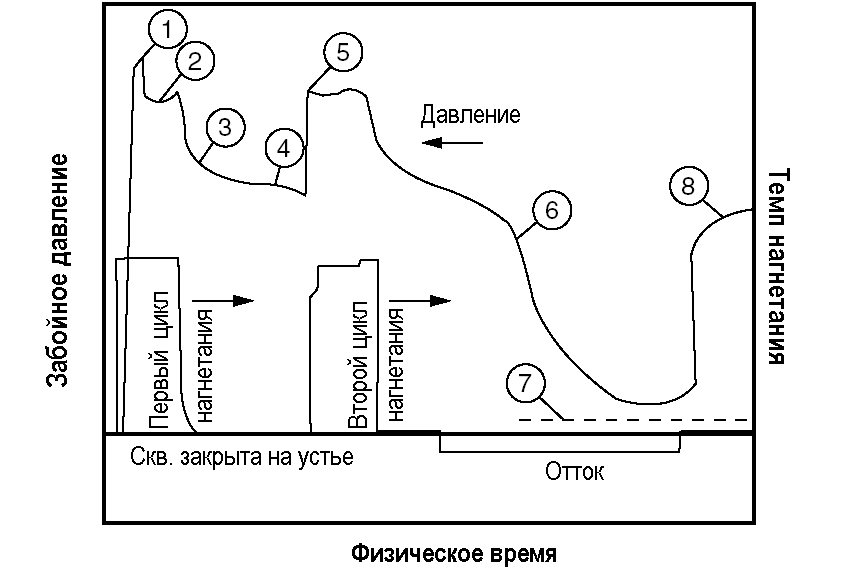
1. Разрыв пласта 2. Распространение трещины 3. Мгновенное давление при закрытом устье 4. Давление смыкания из спада давления 5. Повторное открытие трещины 6. Давление смыкания по оттоку 7. Асимптотическое пластовое давление 8. Давление смыкания по обратному ходу

РИС. 7-1. Ключевые элементы на кривой давления при минифраке.

Закрытие (смыкание) трещины обычно определяют по одному или более построениям кривой спада давления с учетом любой ранее полученной информации (например, данных, полученных при проведении микро-ГРП). Некоторые из наиболее популярных графиков, используемых для идентификации давления закрытия трещины, следующие:

n p_shut-in от t

n p_shut-in от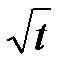

n p_shut-in от g -функции (и варианты)

n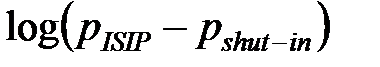

Происхождение и использование этих различных графиков в некоторой мере более интуитивное, нежели теоретическое, что может приводить к неверным результатам. Теоретическое обоснование и ограничения анализа кривых спада давления должны пониматься в контексте конкретных применений. Дополнительные сложности состоят в том, что эффекты температуры и сжимаемости могут вызывать отклонения давления от идеальных кривых. В этом случае можно построить кривые спада с температурными поправками, что позволит нормально проинтерпретировать кривые различных типов [Soliman, 1984].

Исходная концепция анализа кривых спада давления основана на наблюдении, что скорость спада давления в процессе закрытия трещины содержит полезную информацию об интенсивности процесса утечки [Nolte, 1979, Soliman and Daneshy, 1991]. Это противоположно ситуации в период нагнетания, когда на давление влияет множество других факторов.

Если мы примем, что площадь трещины развивалась с постоянным показателем степени 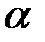и остается постоянной после остановки насосов, то в момент времени 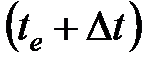объем трещины задается выражением

(7-1)

где приращение безразмерного времени

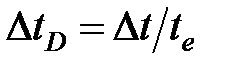(7-2)

а функция двух переменных 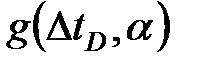может быть определена интегрированием. Ее общий вид дается в [Valkó and Economides, 1995]:

(7-3)

Функция 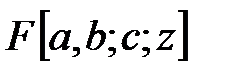— это «гипергеометрическая функция», которая имеется в виде таблиц или расчетных алгоритмов. Для вычислительных целей полезны аппроксимации g -функции, приведенные в таблице 7-1 (напр., они включены в Excel-электронную таблицу MF для анализа минифрака).

Поделив уравнение 7-1 на площадь, получаем ширину трещины в момент времени 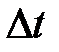после конца закачки:

(7-4)

Отсюда, изменение ширины трещины во времени определяется функцией 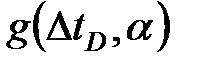, продолжительностью периода нагнетания и коэффициентом утечки, но площадь трещины на нее не влияет.

Уменьшение средней ширины невозможно наблюдать непосредственно, но эффективное давление во время закрытия трещины уже прямо пропорционально средней ширине согласно выражению

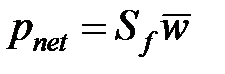(7-5)

просто потому, что пласт описывается теорией линейной упругости (т.е., уравнением 4-2). Коэффициент 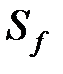— это жесткость трещины, выражаемая в Па/м (psi/фут). Обратная ей величина, , называется податливостью трещины. Для основных типов геометрии трещины выражения для жесткости трещины приведены в таблице 7-2.

Объединение уравнений 7-4 и 7-5 дает следующее выражение [Nolte, 1979]:

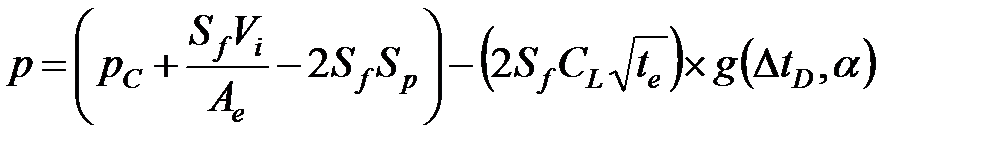(7-6)

ТАБЛИЦА 7-1. Аппроксимация g -функции для различных показателей степени a

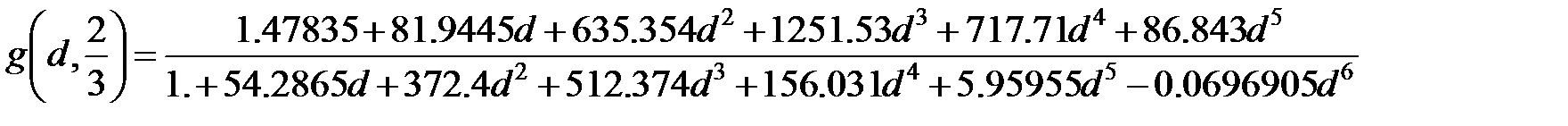
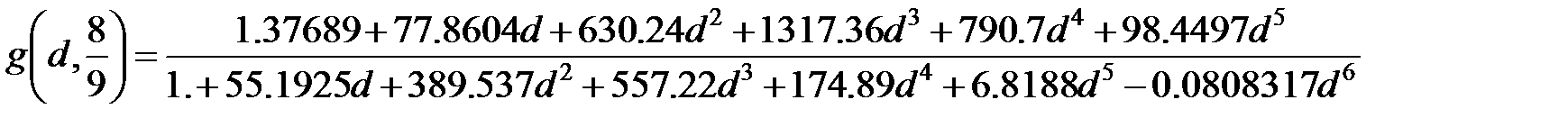
ТАБЛИЦА 7-2. Константа пропорциональности, Sf, и предлагаемые значения a для различных типов геометрии трещины
	PKN	KGD	Radial Радиальная

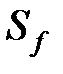
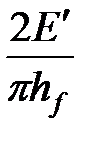
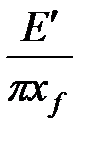
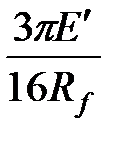
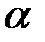
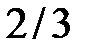
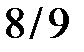
Уравнение 7-6 показывает, что спад давления в период закрытия на устье будет следовать тренду в виде прямой,

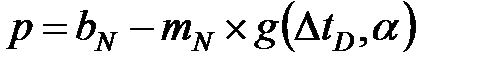(7-7)

если построить его в зависимости от g -функции (т.е., преобразованного времени, [Castillo, 1987]). Значения g -функции должны быть построены с показателем степени 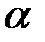, который считается действительным для данной модели. Угловой коэффициент прямой, 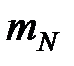, связан с неизвестным коэффициентом утечки следующим выражением:

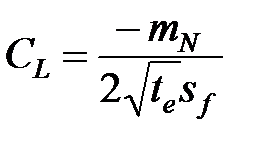(7-8)

Подставив соответствующее выражение для жесткости трещины, можно оценить коэффициент поглощения, как дано в таблице 7-3. В этой таблице показано, что расчетный коэффициент утечки для геометрии PKN не зависит от неизвестных величин, так как время нагнетания, высота трещины и модуль плоской деформации считаются известными. Для двух других рассмотренных типов геометрии эта же процедура приводит к оценке коэффициента утечки, которая сильно зависит от продольного размера трещины (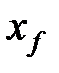 или ).

Из уравнения 7-6 мы видим, что влияние мгновенной утечки сосредоточено в точке пересечения прямой с осью g = 0:

(7-9)

ТАБЛИЦА 7-3. Коэффициент поглощения и продольный размер трещины при нулевой утечке для различных типов геометрии трещины
	PKN	KGD	Radial Радиальная
Коэффициент утечки,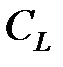
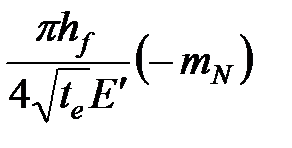
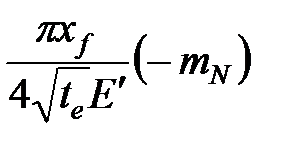
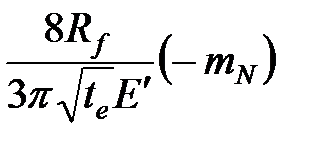
Продольный размер трещины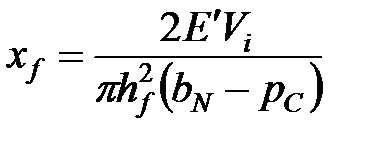

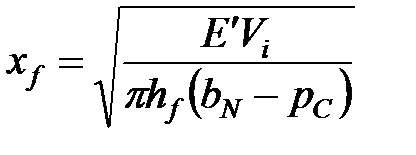
Как предложил Шляпоберский [Shlyapobersky, 1987], уравнение 7-9 может быть использовано для определения неизвестного продольного размера трещины, если мы принимаем, что мгновенной утечки нет. Вторая строка таблицы 7-3 показывает оценки продольного размера трещины для трех основных моделей. Отметьте, что допущение об отсутствии мгновенной утечки дает оценку длины трещины для геометрии PKN, но это значение не используется для получения коэффициента утечки. Для моделей KGD и радиальной — сначала рассчитывается продольный размер трещины, а затем он используется для интерпретации наклона кривой (т.е., для определения ). Когда становятся известны продольный размер трещины и коэффициент утечки, потерянная ширина в конце нагнетания может быть легко определена из выражения

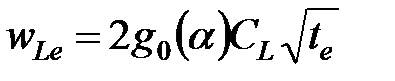(7-10)

Ширина трещины равна

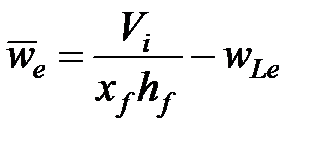(7-11)

для двух прямоугольных моделей и

(7-12)

для радиальной модели.

Часто также определяют эффективность (коэффициент использования) жидкости:

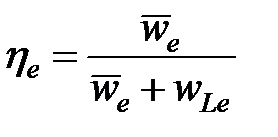(7-13)

Отметьте, что продольный размер трещины и эффективность являются параметрами состояния, то есть они будут иметь различные значения для минифрака и для основного ГРП. Только коэффициент утечки есть параметр модели, который может быть перенесен с минифрака на основной ГРП, но даже после этого необходима некоторая осторожность в его интерпретации. Объемный коэффициент утечки, определенный по вышеописанному методу, является «кажущимся» относительно поверхности трещины. Если мы имеем информацию о проницаемой высоте (мощности), 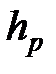, и из нее следует, что только часть трещины приходится на проницаемый пласт, то кажущийся коэффициент утечки следует преобразовать в «истинное» значение, относящееся только к проницаемой площади. Чтобы сделать это, нужно просто поделить кажущееся значение на 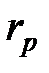(см. уравнение7-14).

Хотя описанная процедура подходит для многих ГРП в низкопроницаемых пластах, она может давать неверные результаты для пластов более высокой проницаемости. Стандартная интерпретация минифрака определяет один эффективный коэффициент утечки жидкости, который обычно немного завышает утечку жидкости, будучи экстраполирован на полнообъемный ГРП (рис. 7-2).

Это завышение обычно обеспечивает дополнительный коэффициент безопасности в низкопроницаемых пластах, помогающий предотвратить закупорку трещины проппантом. Однако та же самая методика, примененная при высокой проницаемости, или же при большой разности давления между трещиной и пластом, может значительно завышать поглощение для жидкостей, образующих фильтрационную корку (рис. 7-3, [Dusterhoft, 1995]).

Завышение расчетной утечки жидкости может сильно повредить, когда целью является плучение концевого экранирования в точно рассчитанное время. В этом случае альтернативой классического анализа спада давления является моделирование как мгновенной утечки, так и комбинированного коэффициента утечки путем подбора теоретической кривой эффективного давления при помощи трехмерной моделирующей компьютерной программы. Этот подход проиллюстрирован на рис. 7-4.

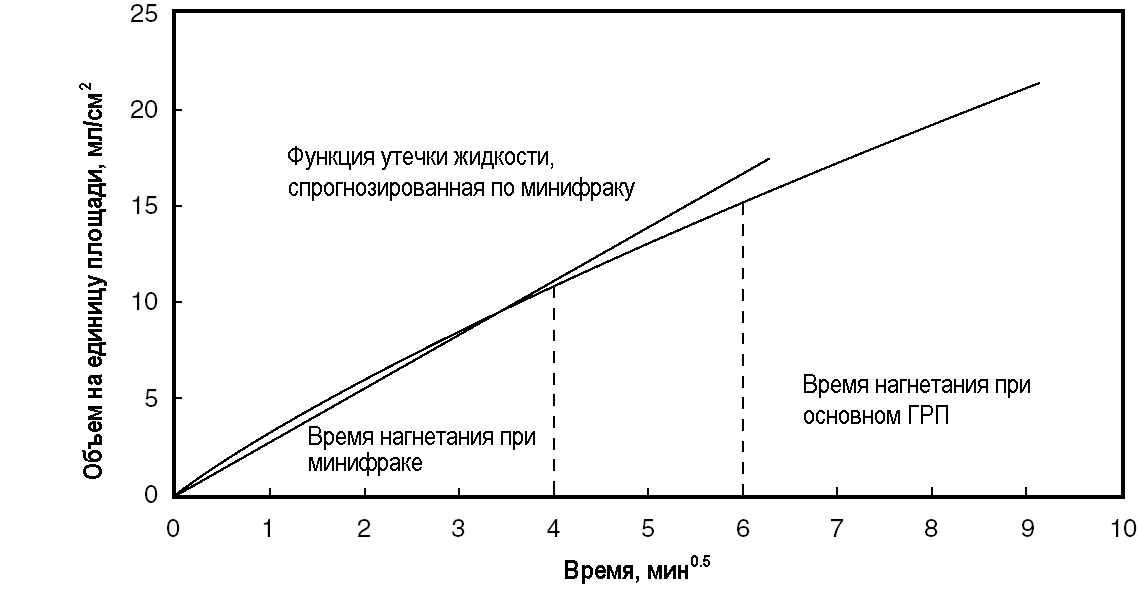
РИС. 7-2. Поглощение жидкости, экстраполированное на полный объем ГРП, низкая проницаемость.

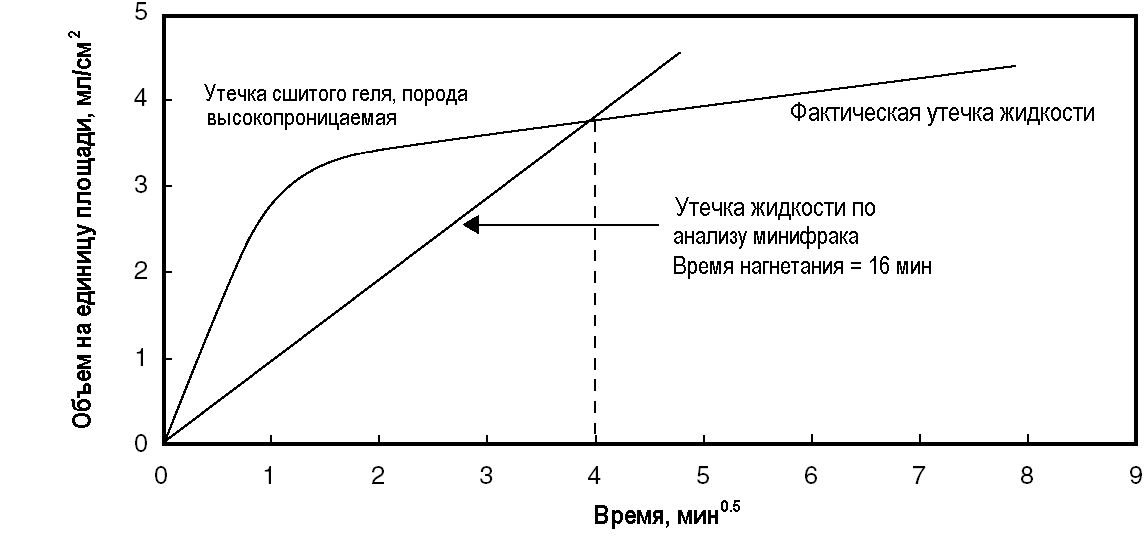
РИС. 7-3. Завышение утечки жидкости при экстраполяции на полный объем ГРП, высокая проницаемость.

Отметьте, что введение более чем одного параметра утечки (и других настраиваемых переменных) увеличивает число степеней свободы. Хотя при этом обычно может быть достигнута лучшая аппроксимация наблюденных давлений, решение часто становится неоднозначным (т.е., такая же сходимость может быть достигнута при других значениях тех же параметров).

РИС. 7-4. Утечка, рассчитанная на основе подбора кривой давления на трехмерном симуляторе (моделирующей программе) (Источник: [Dusterhot et al., 1995]).

Не нашли, что искали? Воспользуйтесь поиском: